1201. Algorithm - SortingSorting
Classic sorting algorithms.
1. Common Sorting Algorithms
| Name | Average | Best Case | Worst Case | Space Complexity | Stable |
|---|---|---|---|---|---|
| Bubble Sort | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | Yes |
| Insertion Sort | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | Yes |
| Shell Sort | Depends | $O(n\log{}n)$ | Depends | $O(1)$ | No |
| Selection Sort | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | No |
| Heap Sort | $O(n\log{}n)$ | $O(n\log{}n)$ | $O(n\log{}n)$ | $O(1)$ | No |
| Merge Sort | $O(n\log{}n)$ | $O(n\log{}n)$ | $O(n\log{}n)$ | $O(n)$ | Yes |
| Quick Sort | $O(n\log{}n)$ | $O(n\log{}n)$ | $O(n^2)$ | $O(\log{}n)$ | No |
| Bucket Sort | – | $O(n+r)$ | $O(n+r)$ | $O(n+r)$ | Yes |
| Counting Sort | – | $O(n+r)$ | $O(n+r)$ | $O(n+r)$ | Yes |
| Radix Sort | – | $O(nk/d)$ | $O(nk/d)$ | $O(n+2^d)$ | Yes |
2. Bubble Sort
2.1 How It Works?
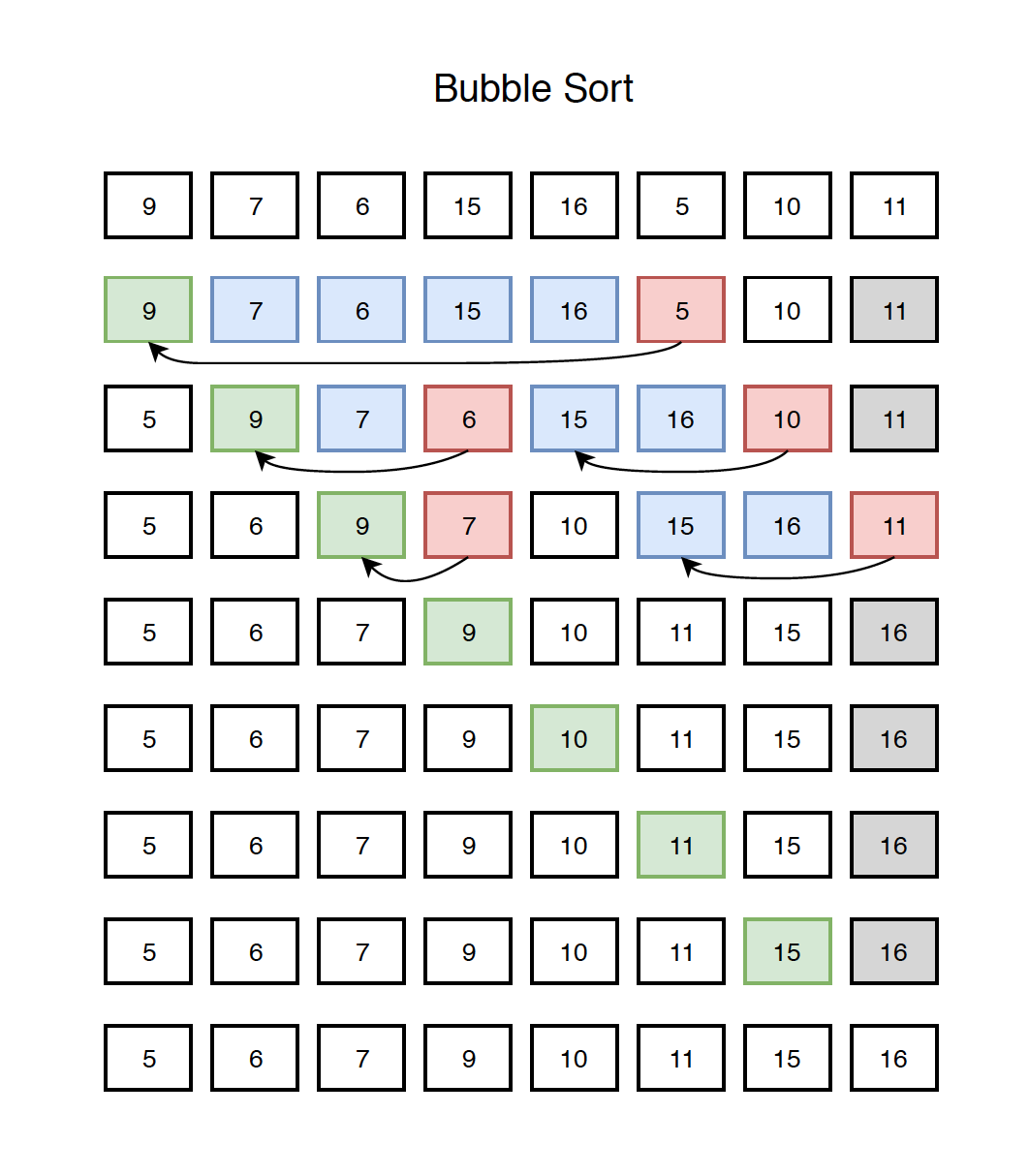
Each time, start taking the last element and compare it with the previous one, swap them if the latter is smaller than the former. By doing this repetitively, bubble up the smallest element and append it to the sorted head list.
2.2 Implementation
public void bubbleSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
for(int i = 0; i < nums.length; i++) {
for (int j = nums.length - 1; j > i; j--) {
if (nums[j] < nums[j - 1]) {
int temp = nums[j];
nums[j] = nums[j - 1];
nums[j - 1] = temp;
}
}
}
}
2.3 Complexity
- Space: $O(1)$
- Time: Average $O(n^2)$, Worst Case $O(n^2)$
3. Insertion Sort
3.1 How It Works?
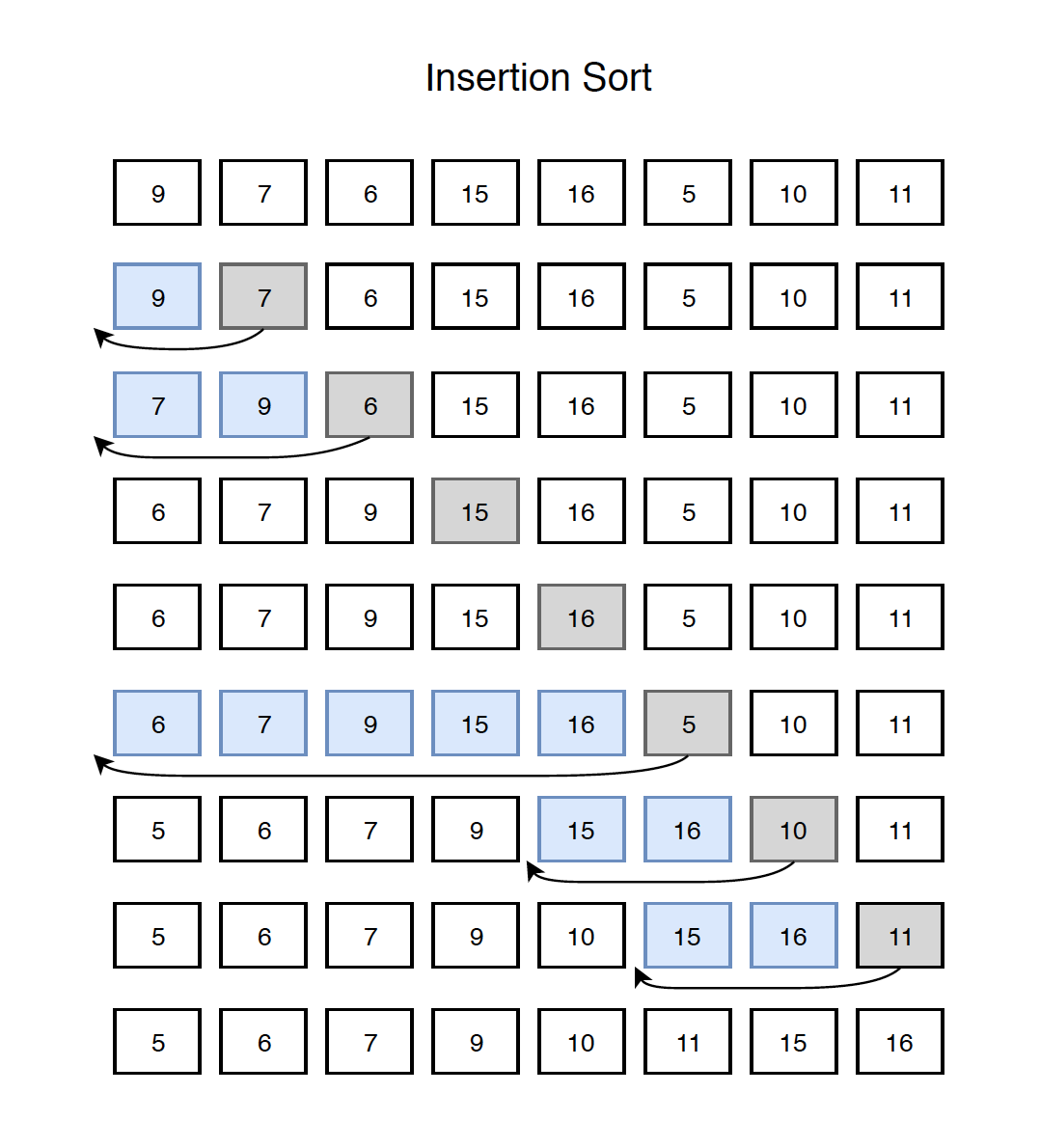
Start from the second element, compare it with the previous one. Swap them if the latter is larger than the former, otherwise, stop comparing, move to the next element. By doing this repetitively, we always take the first element for the unsorted tail list and insert it to the proper position of sorted head list.
2.2 Implementation
public void insertionSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
for (int i = 1; i < nums.length; i++) {
int key = nums[i];
int j = i;
while (j > 0 && nums[j - 1] > key) {
nums[j] = nums[j - 1];
j--;
}
nums[j] = key;
}
}
3.3 Complexity
- Space: $O(1)$
- Time: Average $O(n^2)$, Worst Case $O(n^2)$
4. Shell Sort
4.1 How It Works?
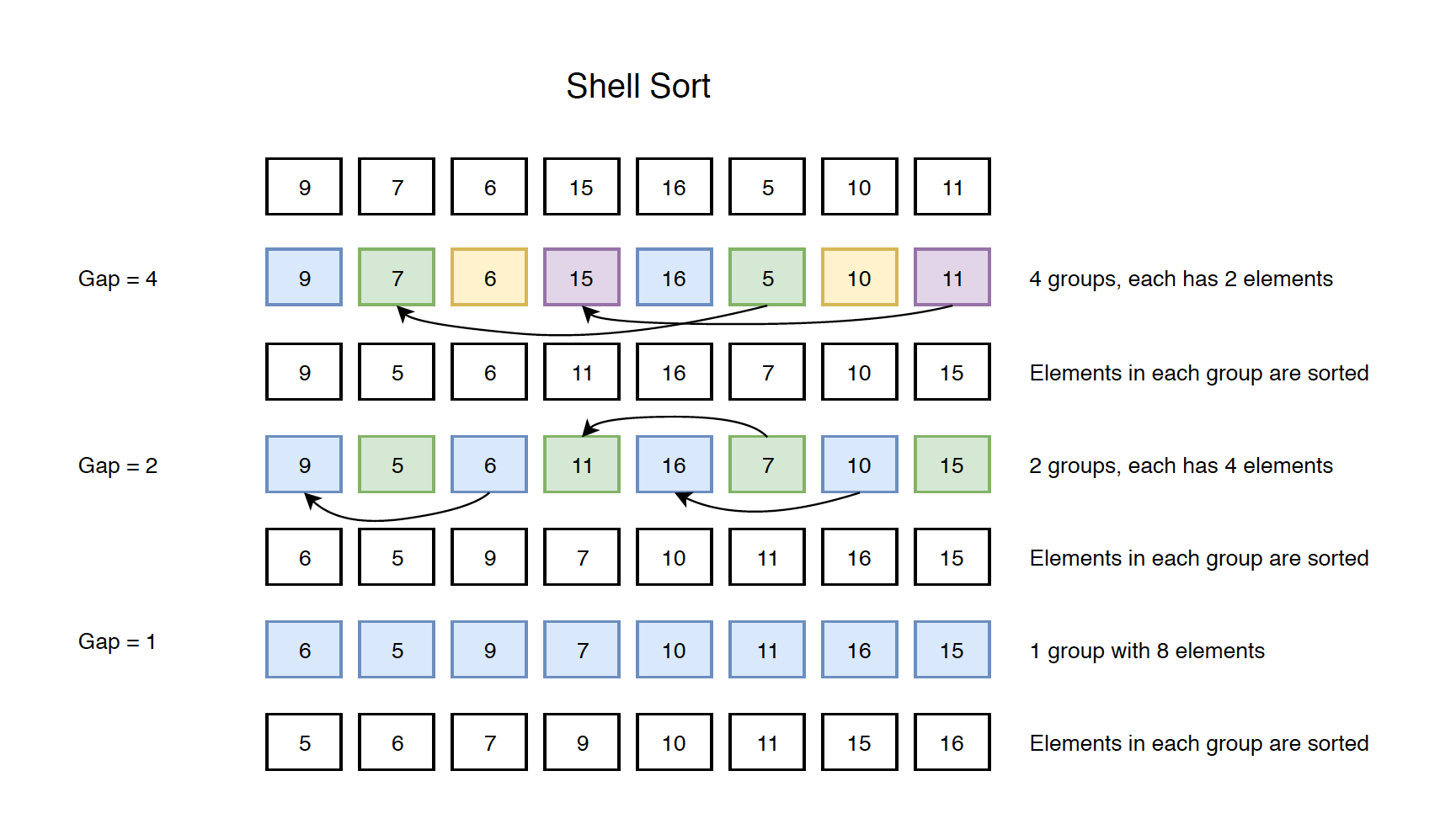
Swap two items who has the distance of the gap. Gap is reduced by half in every iteration, until it becomes to one.
4.2 Implementation
public void shellSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
for (int gap = nums.length / 2; gap > 0; gap = gap / 2) {
for (int i = gap; i < nums.length; i++) {
int temp = nums[i];
int j;
for (j = i; j >= gap && nums[j - gap] > temp; j = j - gap) {
nums[j] = nums[j - gap];
}
nums[j] = temp;
}
}
}
4.3 Complexity
- Space: $O(1)$
- Time: The above implementation has average $O(n^2)$, worst Case $O(n^2)$. There are other ways to reduce gap which lead to better time complexity.
5. Selection Sort
5.1 How It Works?
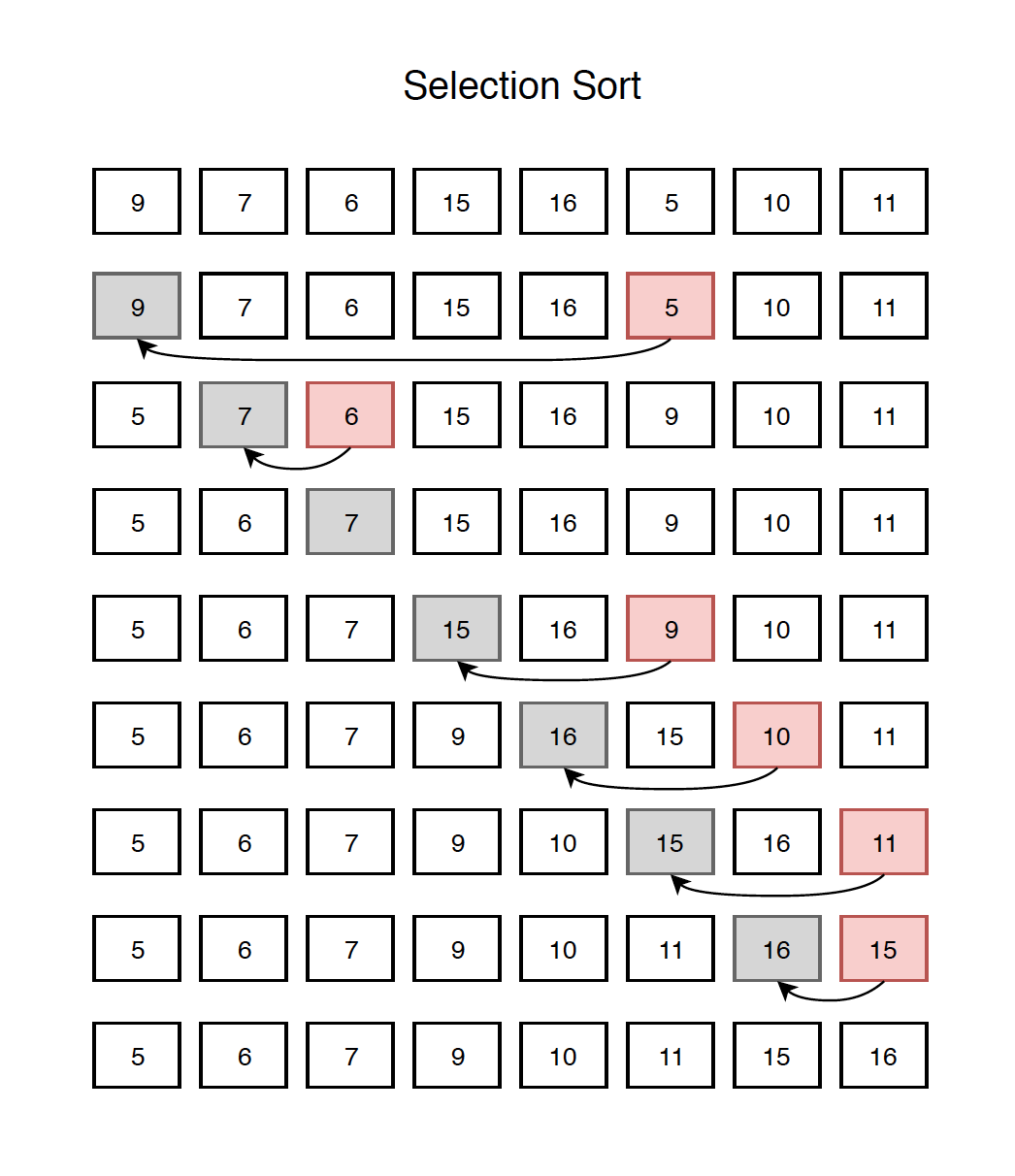
Start from the first element, each time, find the smallest element after this element. Swap it with current element if it is smaller. By doing this repetitively, we always select the smallest element in the unsorted tail list and append it to the end of the sorted head list.
5.2 Implementation
public void selectionSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
for (int i = 0; i < nums.length; i++) {
int min = i;
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] < nums[min]) {
min = j;
}
}
if (min > i) {
int temp = nums[i];
nums[i] = nums[min];
nums[min] = temp;
}
}
}
5.3 Complexity
- Space: $O(1)$
- Time: Average $O(n^2)$, Worst Case $O(n^2)$
6. Heap Sort
6.1 How It Works?
1) Build a max heap with the given array.
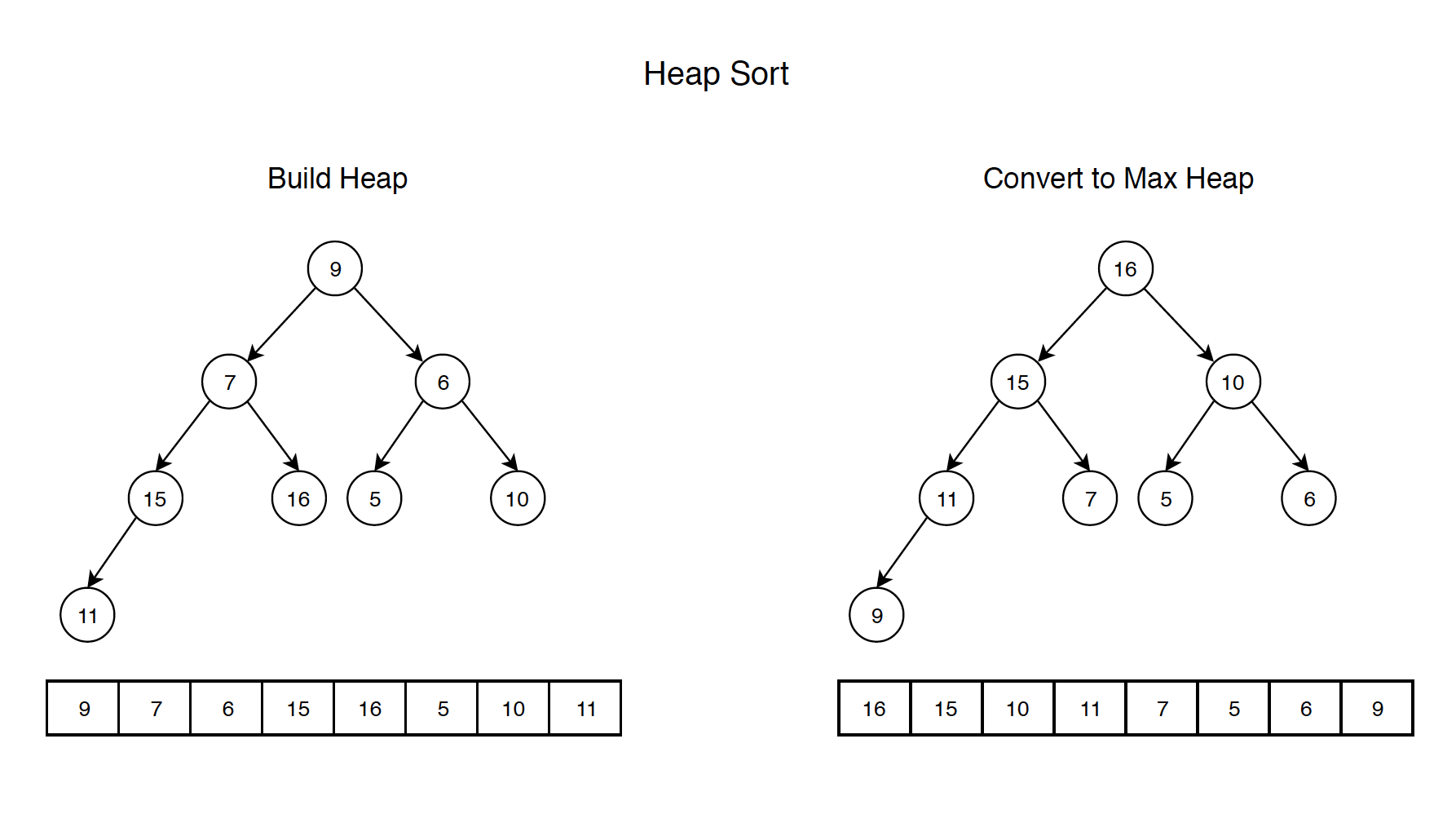2) The root contains the largest item. Swap root with last node, remove the last node(the largest item), then heapify the new root. The following diagrams shows how to use heap to find the largest and the second largest items.
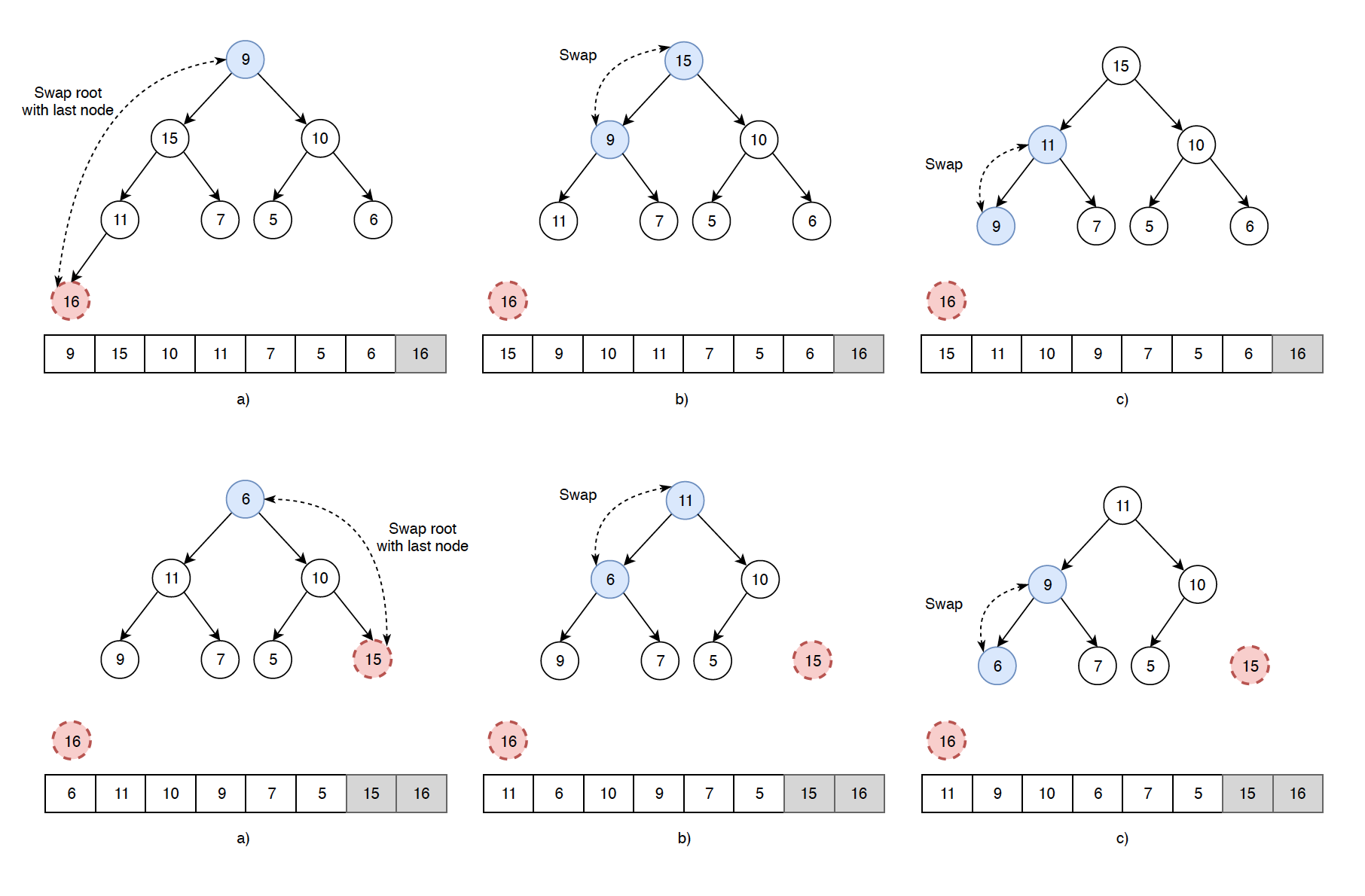3) Repeat above steps while size of heap is greater than 1. Below is the entire sorting process.
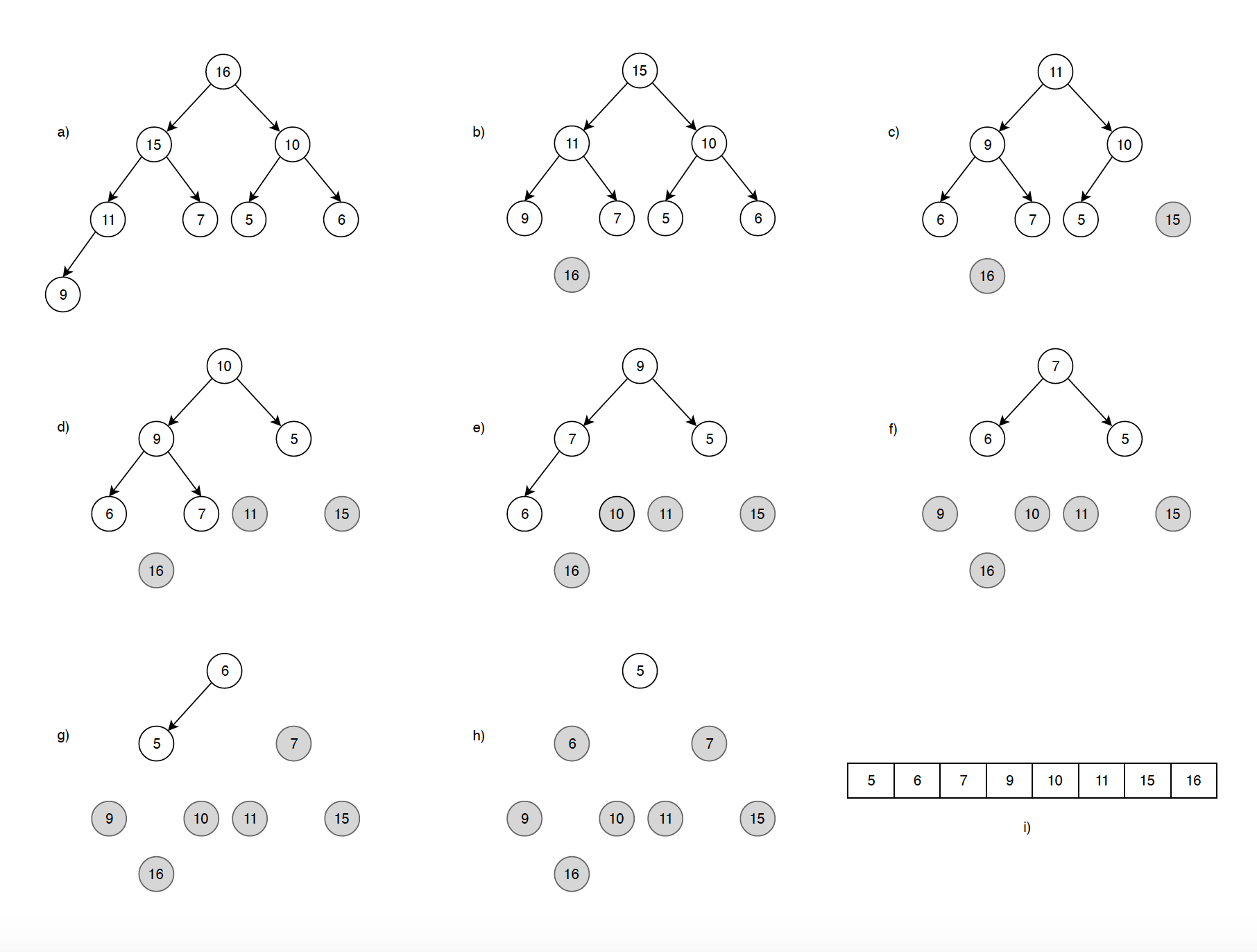
6.2 Implementation
public void heapSort(int nums[]) {
if (nums == null || nums.length < 2) {
return;
}
// Build heap (rearrange array)
for (int i = nums.length / 2 - 1; i >= 0; i--) {
heapify(nums, nums.length, i);
}
// One by one extract an element from heap
for (int i = nums.length - 1; i >= 0; i--) {
int temp = nums[0];
nums[0] = nums[i];
nums[i] = temp;
heapify(nums, i, 0);
}
}
/*
* n is the size of heap, i is the index of node in array
*/
private void heapify(int nums[], int n, int i) {
int largest = i; // Initialize largest as root
int left = 2*i + 1; // left child
int right = 2*i + 2; // right child
// If left child is larger than root
if (left < n && nums[left] > nums[largest]) {
largest = left;
}
// If right child is larger than largest so far
if (right < n && nums[right] > nums[largest]) {
largest = right;
}
// If largest is not root
if (largest != i) {
int swap = nums[i];
nums[i] = nums[largest];
nums[largest] = swap;
// Recursively heapify the affected sub-tree
heapify(nums, n, largest);
}
}
6.3 Complexity
- Space: $O(n\log{}n)$
- Time: Average $O(n\log{}n)$, Worst Case $O(n\log{}n)$
7. Merge Sort
7.1 How It Works?
Binary split the original arrays to smaller groups until each group contains only one element. Then, binary merge these groups to larger groups until we have the final one group with all sorted elements.
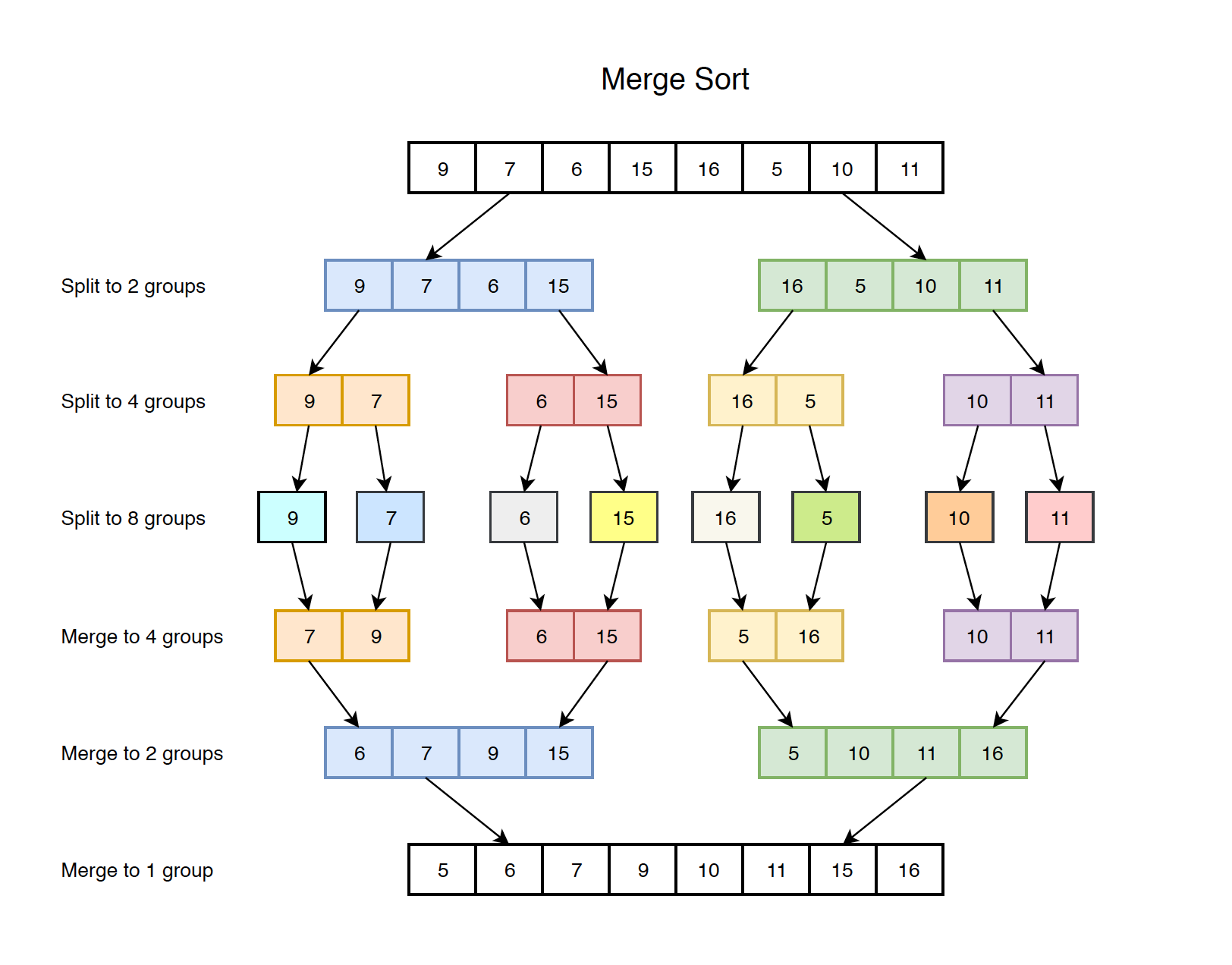
7.2 Implementation
public void mergeSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
mergeHelper(nums, 0, nums.length - 1);
return;
}
private void mergeHelper(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int mid = start + (end - start) / 2;
mergeHelper(nums, start, mid);
mergeHelper(nums, mid + 1, end);
merge(nums, start, mid, end);
}
private void merge(int[] nums, int start, int mid, int end) {
int[] copy = Arrays.copyOf(nums, nums.length);
int left = start;
int right = mid + 1;
for (int k = start; k <= end; k++) {
if (left > mid) { // no item at left
nums[k] = copy[right];
right++;
}
else if(right > end) { // no item at right
nums[k] = copy[left];
left++;
}
else if (copy[left] <= copy[right]) {
nums[k] = copy[left];
left++;
}
else{
nums[k] = copy[right];
right++;
}
}
}
7.3 Complexity
- Space: $O(n)$
- Time: Average $O(n\log{}n)$, Worst Case $O(n\log{}n)$
8. Quick Sort
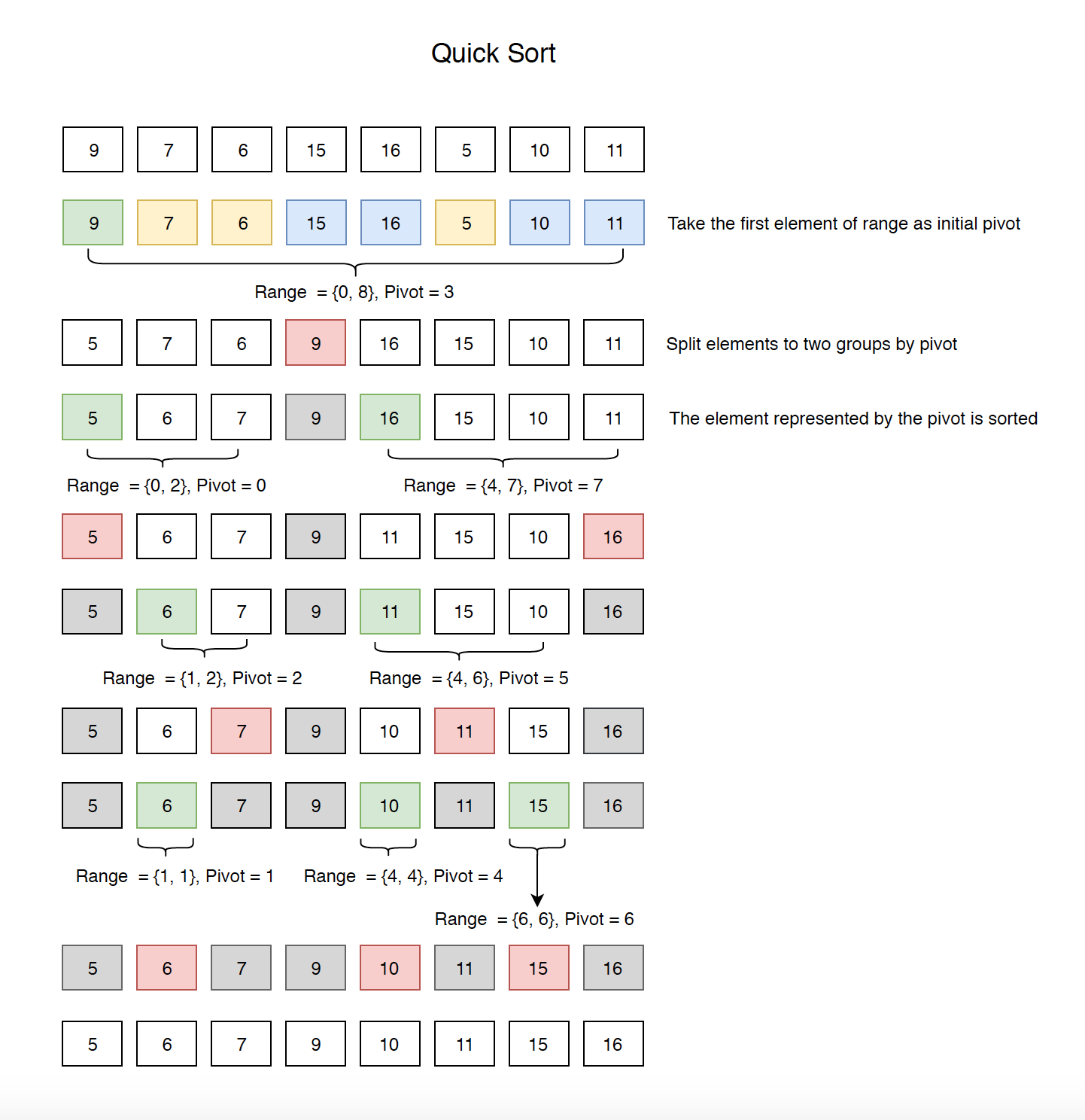
8.1 How It Works?
1) Take the first element as pivot, split the elements to two groups. All elements in first group are smaller than pivot and all elements in second group are larger than pivot.
2) The new position of the pivot is fixed(sorted).
3) Repeat above steps until group contains only one element. Below is the entire sorting process.
8.2 Implementation
public void quickSort(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
quickHelper(nums, 0, nums.length - 1);
return;
}
private void quickHelper(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int pivot = partition(nums, start, end);
quickHelper(nums, start, pivot - 1);
quickHelper(nums, pivot + 1, end);
}
// one way
private int partition(int[] nums, int start, int end) {
int pivot = start; // select the first as the pivot
for (int i = start + 1; i <= end; i++) {
if (nums[i] < nums[start]) {
pivot++;
int temp = nums[pivot];
nums[pivot] = nums[i];
nums[i] = temp;
}
}
int temp = nums[pivot];
nums[pivot] = nums[start];
nums[start] = temp;
return pivot;
}
8.3 Complexity
- Space: $O(n\log{}n)$
- Time: Average $O(n\log{}n)$, Worst Case $O(n^2)$
9. Bucket Sort
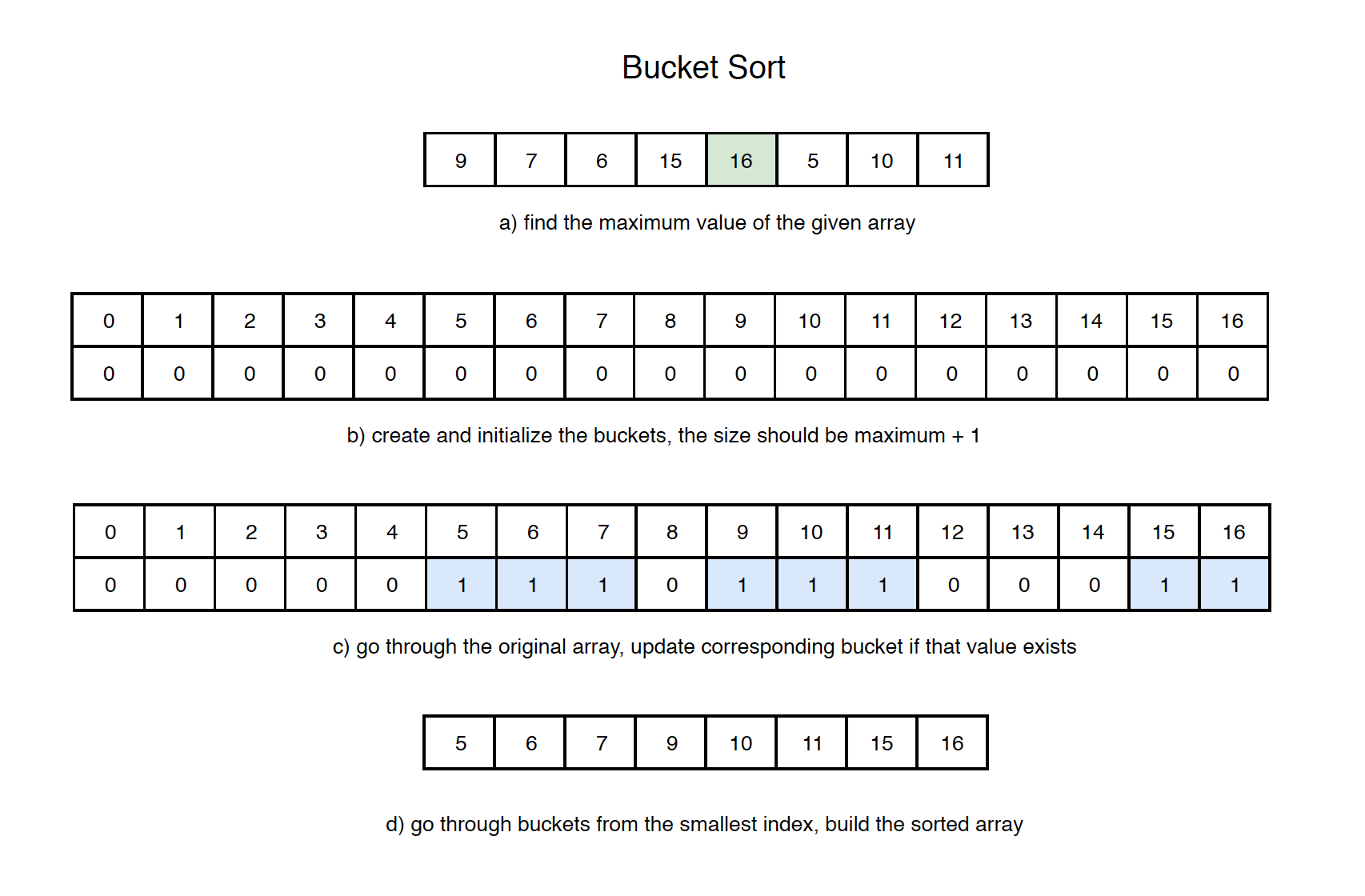
9.1 How It Works?
1) Get the maximum value of the given array.
2) Create and initialize buckets.
3) Go through the original array, update corresponding bucket if that value exists.
4) Go through the buckets from the smallest index, build the sorted array.
9.2 Implementation
public void bucketSort(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
// get the max value
int max = Integer.MIN_VALUE;
for (int i = 0; i < nums.length; i++) {
if (nums[i] > max) {
max = nums[i];
}
}
// create buckets
int [] bucket = new int[max + 1];
// initialize buckets
for (int i = 0; i < bucket.length; i++) {
bucket[i] = 0;
}
// increment bucket value by one if corresponding element is found
for (int i = 0; i < nums.length; i++) {
bucket[nums[i]]++;
}
// rebuild array from buckets
int index = 0;
for (int i = 0; i < bucket.length; i++) {
for (int j = 0; j < bucket[i]; j++) {
nums[index++] = i;
}
}
}
9.3 Complexity
- Space: Depends
- Time: Average $O(n+r)$, Worst Case $O(n+r)$
10. Merge Sort vs Quick Sort
Both Merge Sort and Quick Sort use the divide conquer methodology.
| Feature | Merge Sort | Quick Sort |
|---|---|---|
| Divide Conquer | Yes | Yes |
| Order | Individual sorted first, then overall sorted | Overall sorted first, then individual sorted |
| Time complexity | Divide = O(1), Conquer = O(n), total = nLog(n) | Divide = O(n), Conquer = O(1), total = nlog(n) |
| Space | Require extra space | In-place |
| Stable | Yes | No |
How to explain the time complexity of merge sort?
- It divides array to smaller ones, length from n to n/2, then to n/4, until each group has only 1 item. The total level is log(n).
- At each level, it use O(1) time to split the array and O(n) time to merge.
- We have log(n) levels and we spend O(n) time at each level, so, the total time is O(n) * log(n) = nlog(n).
How to explain the time complexity of quick sort?
- It divides array to smaller ones by the pivot, the length is not fixed, depends on the value of pivot.
- It takes O(n) time to divide the array with pivot, uses O(1) to recursively conquer the sub arrays.
- In average case, like the merge sort, total level is log(n). At each level, it use O(n) time, so, the total time is O(n) * log(n) = nlog(n).
- In worst case(partition the array only one element each time), it needs O(n^2) times to divide the array.