1232. Algorithm - Sqrt DecompositionSqrt Decomposition
Implement Sqrt Decomposition for range search problems.
1. Range Query
1.1 Problem Description
Given an integer array with n elements, find the sum of some elements in range from i to j. This array is mutable, meaning, any element in the array can be modified. So, we have two following operations query and update. The query method should always work even if the array is updated.
- query(i, j) - Find the sum of the elements between indices
iandj(i ≤ j), inclusive. - update(i, val) - Modify the array by updating the element at index
itoval.
1.2 Solutions
There are two solutions for such range query problem. The first solution for this problem is segment tree. The second solution is Sqrt Decomposition.
2. Sqrt Decomposition
Square root(Sqrt) decomposition allows us to answer queries in $O(\sqrt{k})$ time and the implementation is usually simpler than a segment tree.
2.1 Building Blocks
Decompose the array into small blocks. Suppose the array has 9 elements, it can be split into $\sqrt{9}$ = 3 blocks, and we can easily calculate the sum of each block.
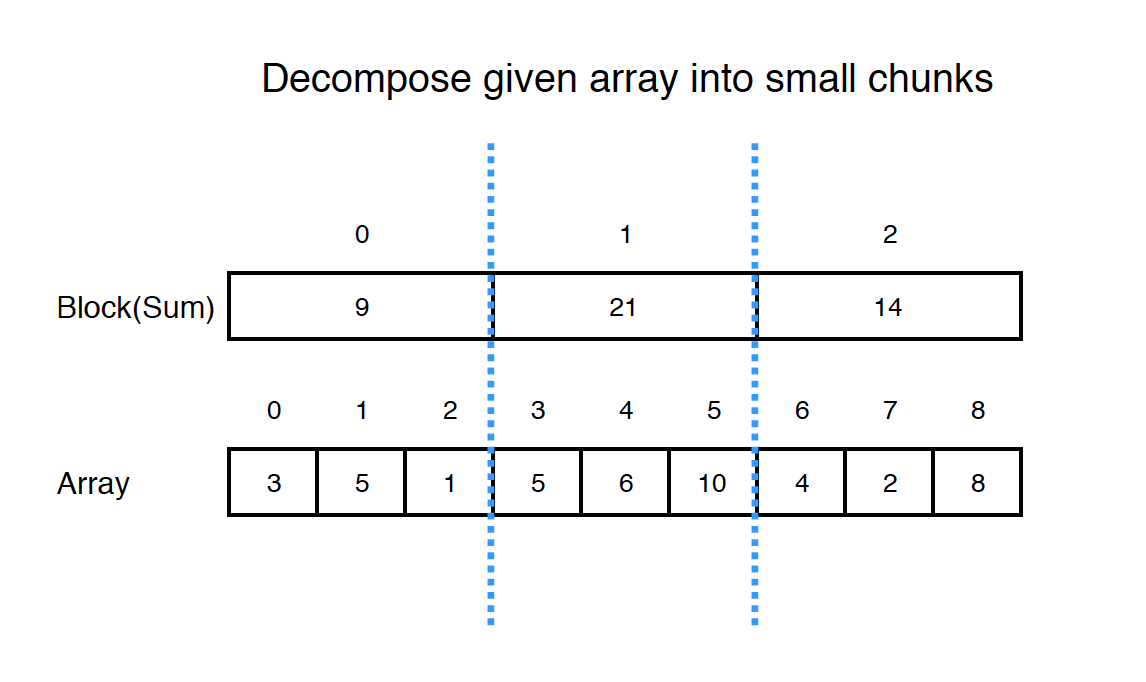
- If the length of the array
nis not a perfect square, then we will have one more block.
2.2 Query
There are two cases for the query.
If range is on block boundaries, we can get the sum from blocks directly. For example, if the range is from 3 to 8, then block[1] and block[2] perfectly cover this range.
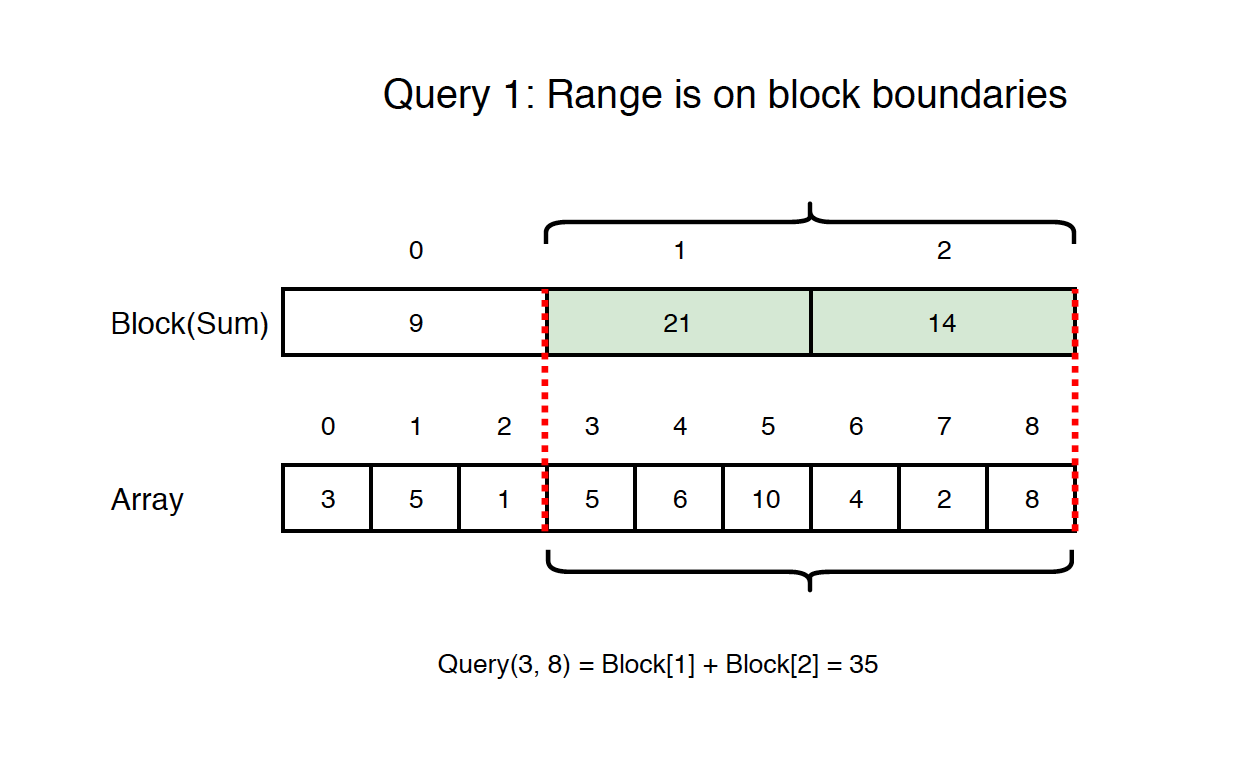 If range crosses blocks partially, we cannot get the sum from blocks directly. For example, if the range is from 2 to 7, we can get the sum for array[3,4,5] from block[1], however, we have to get other sums from the array.
If range crosses blocks partially, we cannot get the sum from blocks directly. For example, if the range is from 2 to 7, we can get the sum for array[3,4,5] from block[1], however, we have to get other sums from the array.
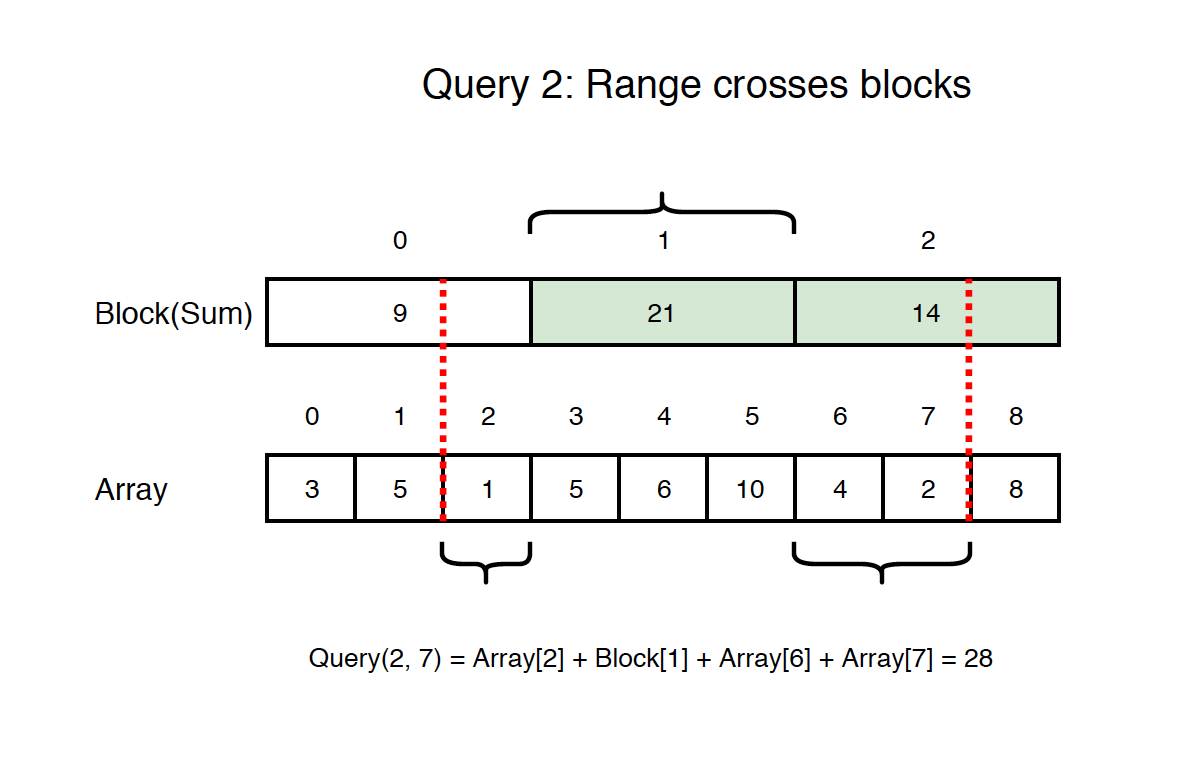
2.3 Update
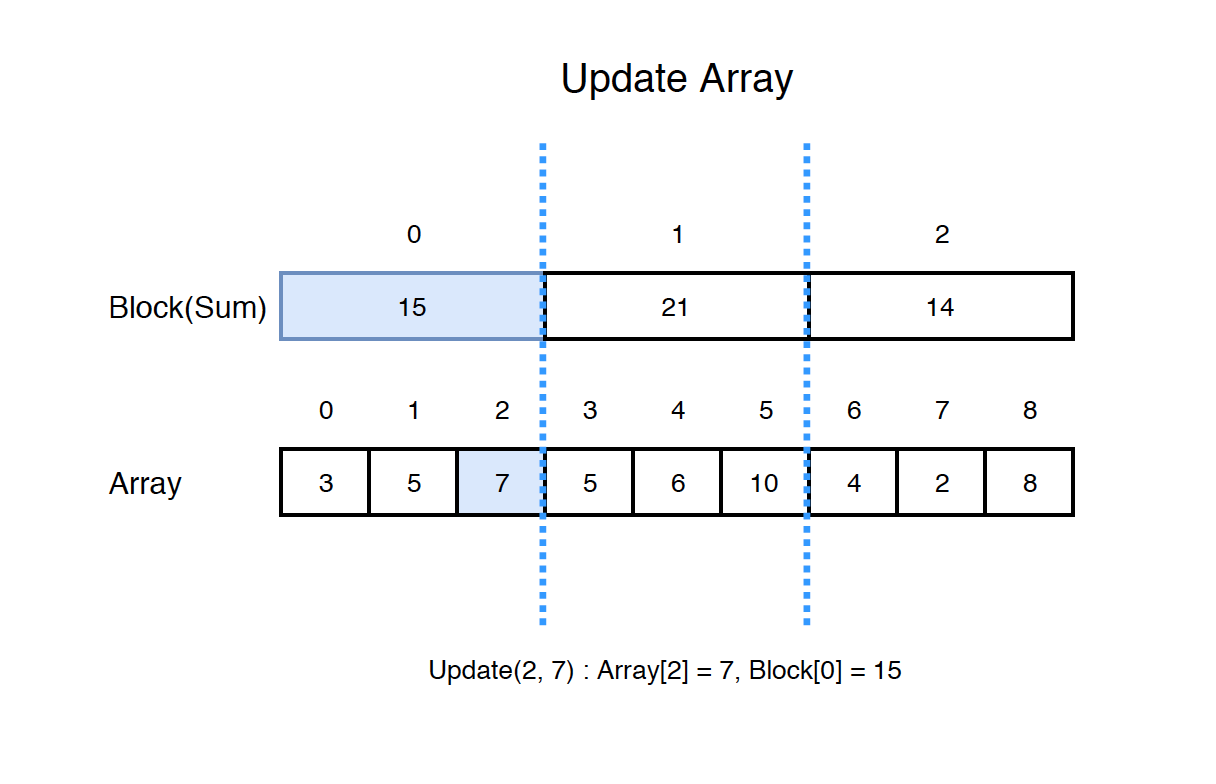
If we update the array, we need to update the block accordingly. For example, update(2,7) will modify the array[2] from 1 to 7, and update block[0] from 9 to 15.
3. Implementation
Implement Sqrt Decomposition with three methods.
- build
- query
- update
public class RangeSearchSum {
private int[] nums;
private long[] sumBlocks;
private int sqrt;
public RangeSearchSum(int[] arr) {
if (arr != null && arr.length > 0) {
build(arr);
}
}
private void build(int[] arr) {
this.sqrt = (int) Math.ceil(Math.sqrt(arr.length));
this.nums = new int[sqrt * sqrt];
System.arraycopy(arr, 0, nums, 0, arr.length); // the tail items in nums may be zero
this.sumBlocks = new long[sqrt];
for (int i = 0; i < sumBlocks.length; i++) {
int startIndex = i * sqrt;
for (int j = 0; j < sqrt; j++) {
sumBlocks[i] += nums[startIndex + j];
}
}
}
// update value by index
public void update(int index, int value) {
int blockIndex = index / sqrt;
sumBlocks[blockIndex] = sumBlocks[blockIndex] - nums[index] + value;
nums[index] = value;
}
// query with left and right indexes
public long query(int left, int right) {
int startBlockIndex = left / sqrt;
int endBlockIndex = right / sqrt;
long sum = 0;
if (startBlockIndex == endBlockIndex) { // in the same block
for (int i = left; i <= right; i++) {
sum += nums[i];
}
} else { // in the different blocks
// overlap
for (int i = startBlockIndex + 1; i < endBlockIndex; i++) {
sum += sumBlocks[i];
}
// left non-overlap
int startIndex = left % sqrt;
for (int i = startIndex; i < sqrt; i++) {
sum += nums[startBlockIndex * sqrt + i];
}
// right non-overlap
int endIndex = right % sqrt;
for (int i = 0; i <= endIndex; i++) {
sum += nums[endBlockIndex * sqrt + i];
}
}
return sum;
}
}
Usage.
RangeSearchSum sd = new RangeSearchSum(new int[] {3,5,1,5,6,10,4,2,8});
sd.query(0, 1); // 8
sd.query(0, 2); // 9
sd.query(3, 5); // 21
sd.query(6, 8); // 14
sd.query(3, 7); // 27
sd.query(2, 7); // 28
sd.query(0, 8); // 44
sd.update(2, 7); // {3,5,7,5,6,10,4,2,8}
sd.query(0, 2); // 15
sd.query(2, 7); // 34
sd.query(6, 7); // 6
sd.query(7, 8); // 10