1212. Algorithm - Two PointersTwo Pointers
Two pointers technique.
1. Two Pointers
Two pointers technique is easy to understand which is generally used to solve problem within linear time complexity.
1.1 Types of Two Pointers
- Collision - One array, move from two sides to middle.
- Forward - One array, both move forward.
- Parallel - Two arrays, each array has been assigned with a pointer.
2. Problem
Given a sorted (in ascending order) integer array nums of n elements and a target value, find if there exists any pair of elements (nums[i], nums[j], i!=j) such that their sum is equal to target.
2.1 Naive Solution
Use two loops to traverse the array to find the matched elements.
// naive solution, O(n^2)
public boolean isPairSumNaive(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return false;
}
for (int i = 0; i < nums.length; i++) {
for (int j = i + 1; j < nums.length; j++) {
if (nums[i] + nums[j] == target) {
return true; // pair exists
}
if (nums[i] + nums[j] > target)
break; // break inner loop as the array is sorted
}
}
// not found
return false;
}
- Time Complexity: $O(n^2)$
2.2 Two Pointers Solution
As the array is sorted, we can use two pointers to solve this problem. One pointer is initially at header, another pointer is initially at tail. Get the sum of the values represented by these two pointers. If sum is equal to target value, then return. If it is smaller than the target, move the left pointer to right; otherwise, move the right pointer to left. Thus, narrow down the scope of the candidates.
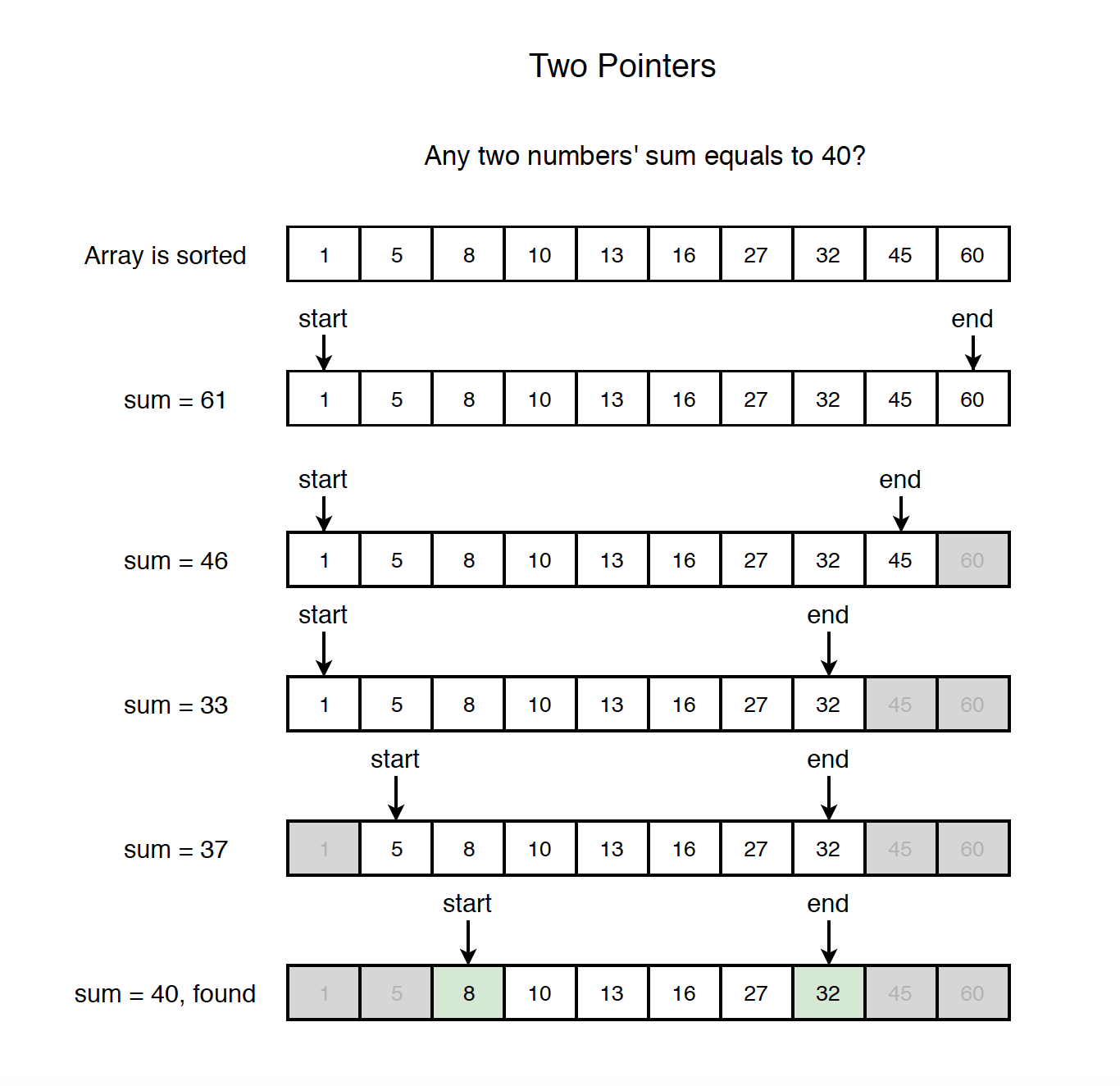See the following implementation.
// Two pointers, O(n)
public boolean isPairSum(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return false;
}
int start = 0;
int end = nums.length - 1;
while (start < end) {
int sum = nums[start] + nums[end];
if (sum == target) {
return true; // pair exists
} else if (sum < target) {
start++; // move start forward to get larger value
} else {
end--; // move end backward to get smaller value
}
}
// not found
return false;
}
- Time Complexity: $O(n)$
3. Classic Problems
3.1 Collision
Sub type: Two Sum
- LeetCode 167 - Two Sum II - Input array is sorted
- LeetCode 15 - 3Sum (Sort + Loop + Two Pointers)
- LeetCode 16 - 3Sum Closest (Sort + Loop + Two Pointers + diff)
- LeetCode 18 - 4Sum (Sort + Double Loop + Two Pointers + HashSet)
- LeetCode 611 - Valid Triangle Number
- LeetCode 42 - Trapping Rain Water
- LeetCode 11 - Container With Most Water
Sub type: Partition
- LintCode 31 - Partition Array(Quick sort)
- LeetCode 125 - Valid Palindrome
- LeetCode 75 - Sort Colors
- LintCode 373 - Partition Array by Odd and Even
- LintCode 49 - Sort Letters by Case
3.2 Forward
Sub type: Window
- LeetCode 209 - Minimum Size Subarray Sum
- LeetCode 3 - Longest Substring Without Repeating Characters (HashMap + Two Pointers)
- LeetCode 76 - Minimum Window Substring (HashMap + Two Pointers)
- LeetCode 159 - Longest Substring with At Most Two Distinct Characters (HashMap + Two Pointers)
- LeetCode 340 - Longest Substring with At Most K Distinct Characters
- LeetCode 19 - Remove Nth Node From End of List (One pass, moving window, linked list)
Sub type: fast and slow
- LeetCode 876 - Middle of the Linked List(second middle node)
- LeetCode 141 - Linked List Cycle
- LeetCode 142 - Linked List Cycle II
3.3 Parallel
Two arrays, one pointer each.
Others- Todo
- LeetCode 26 - Remove Duplicates from Sorted Array
- LeetCode 186 - Reverse Words in a String II
- LeetCode 189 - Rotate Array
- LeetCode 238 - Product of Array Except Self