1141. Data Structure - GraphGraph, DFS, and BFS
Implement undirected graph.
1. Graph
1.1 Definition of Graph
Graph is a data structure that consists of following two components: vertex and edge.
- A finite set of vertices, also called as nodes.
- A finite set of ordered pair of the form (u, v), also called as edge. The pair is ordered because (u, v) is not same as (v, u) in case of a directed graph(di-graph). The pair of the form (u, v) indicates that there is an edge from vertex u to vertex v. The edges may contain weight/value/cost.
Following is an example of an undirected graph with 5 vertices.
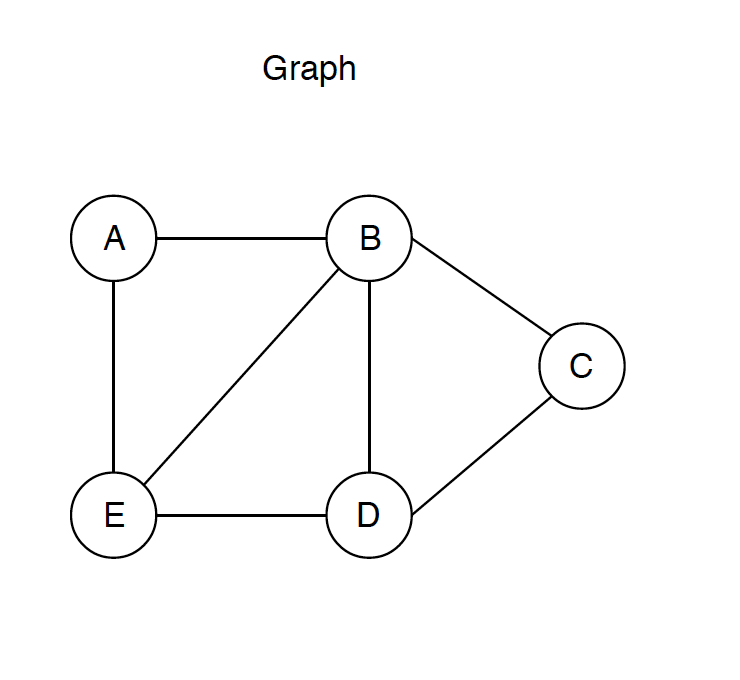
1.2 Graph Features
- Graphs can be either
directedorundirected. While directed edges are like a one-way street, undirected edges are like a two-way street. - Graph might consist of multiple isolated subgraphs. If there is a path between every pair of vertices, it is called a ‘connected graph’.
- Graph can also have cycles (or not). An ‘acyclic graph’ is one without cycles.
2. Implementation of Graph
There are two most common ways to implement graph:
- Adjacency Matrix
- Adjacency List
2.1 Adjacency Matrix
Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be matrix[][], a slot matrix[i][j] = 1 indicates that there is an edge from vertex i to vertex j. Adjacency matrix for undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If matrix[i][j] = w, then there is an edge from vertex i to vertex j with weight w.
The adjacency matrix for the above example graph is:
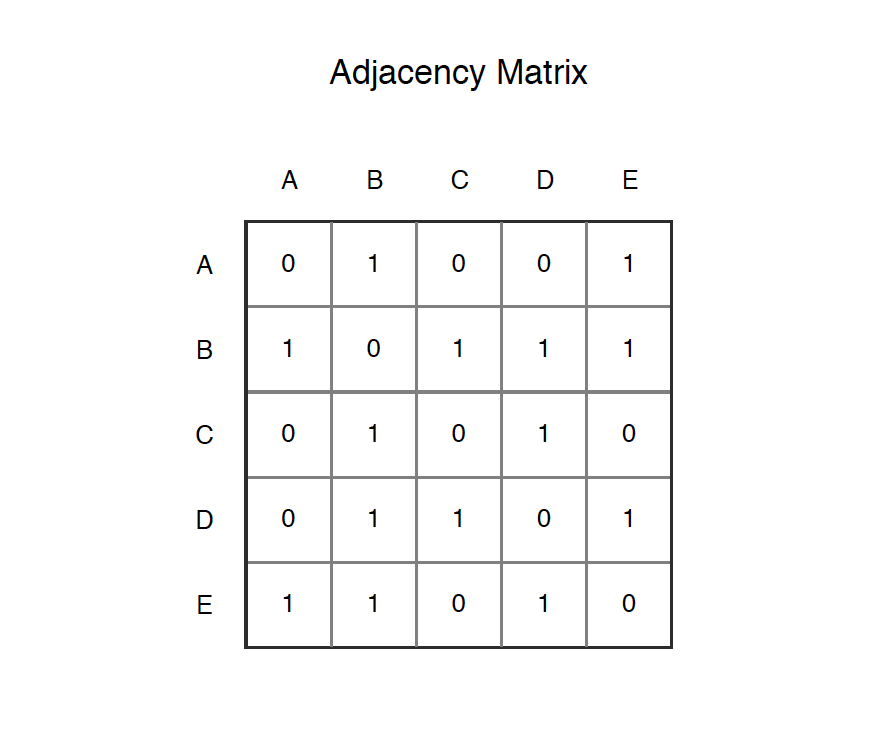
- Pros: Representation is easier to implement and follow. Removing an edge takes $O(1)$ time. Queries like whether there is an edge from vertex ‘u’ to vertex ‘v’ are efficient and can be done $O(1)$.
- Cons: Consumes more space $O(V^2)$. Even if the graph is sparse(contains less number of edges), it consumes the same space. Adding a vertex is $O(V^2)$ time, as you have to rebuild the matrix.
Below is the sample code which implements Graph with Adjacency Matrix.
public class Vertex {
public int index;
public String name;
public boolean visited;
public Vertex(int index, String name) {
this.index = index;
this.name = name;
this.visited = false;
}
@Override
public String toString() {
return name;
}
}
public class AdjMatrixGraph {
private int[][] matrix; // adjacency matrix
private Vertex[] vertices; // array of vertices
private int size; // current number of vertices
public AdjMatrixGraph(int capacity)
{
matrix = new int[capacity][capacity];
vertices = new Vertex[capacity];
size = 0;
// initialize matrix
for (int i = 0; i < capacity; i++) {
for (int j = 0; j < capacity; j++) {
matrix[i][j] = 0;
}
}
}
public void addVertex(String name) {
int index = size++;
vertices[index] = new Vertex(index, name);
}
public void addEdge(int start, int end) {
matrix[start][end] = 1;
matrix[end][start] = 1;
}
}
2.2 Adjacency List
Adjacency List an array of lists. Size of the array is equal to the number of vertices. Let the array be vertexList[]. An entry vertexList[i] represents the list of vertices adjacent to the $i^{th}$ vertex.
Following is adjacency list representation of the above graph.
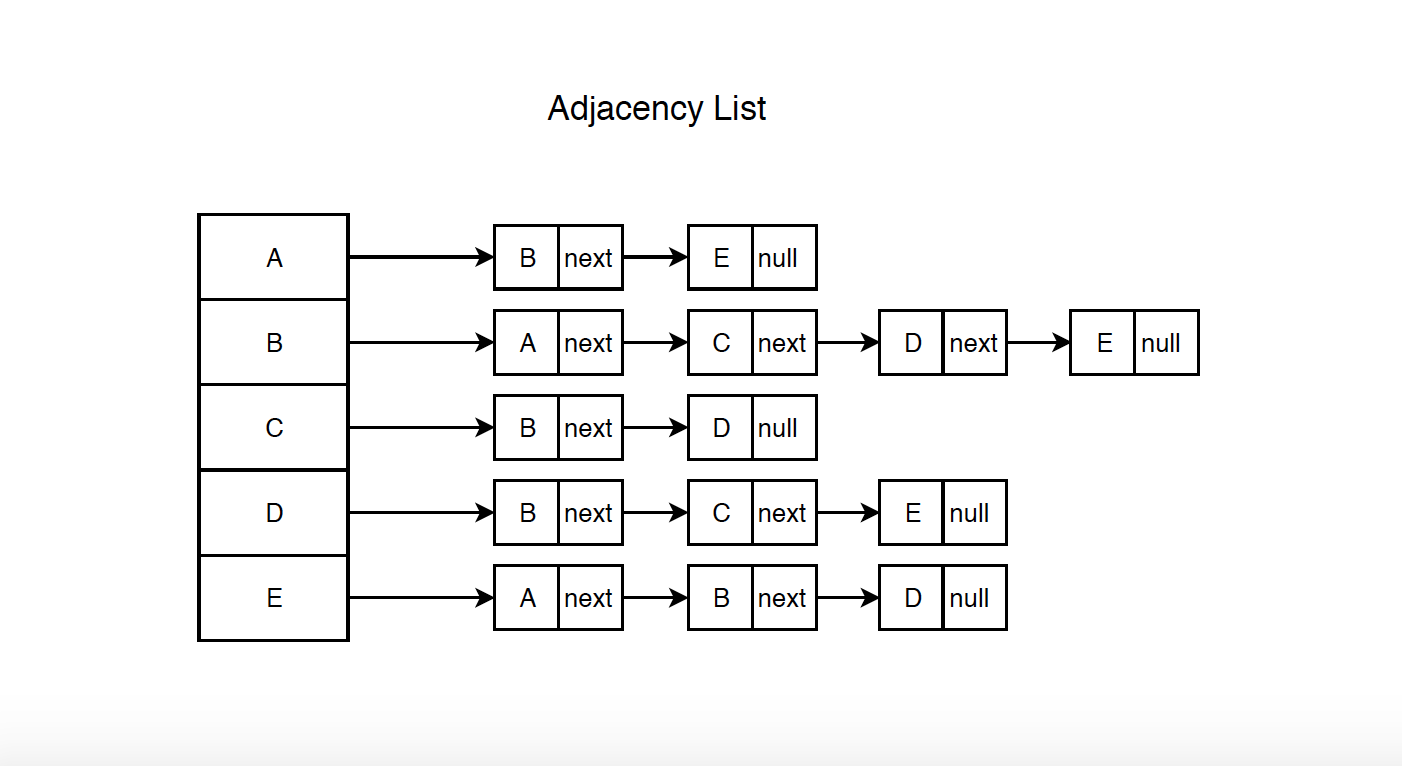
- Pros: Saves space. Generally, it takes $O(V+2E)$, V is number of vertices and E is the number of edges. In the worst case, there can be $V^2$ number of edges in a graph(Every vertex connects to all other vertices) thus consuming $O(V^2)$ space. Adding a vertex is easier, just append a new node into the vertex list.
- Cons: Queries like whether there is an edge from vertex u to vertex v are not efficient and can be done $O(V)$, as you have to search one by one in the vertex list.
Below is the sample code which implements Graph with Adjacency List.
public class AdjListGraph {
private LinkedList<Vertex>[] vertexList; // list of adjacency vertex
private Vertex[] vertices; // array of vertices
private int size; // current number of vertices
public AdjListGraph(int capacity)
{
vertexList = new LinkedList[capacity];
vertices = new Vertex[capacity];
size = 0;
// initialize array
for (int i = 0; i< vertexList.length; i++) {
vertexList[i] = new LinkedList<Vertex>();
}
}
public void addVertex(String name) {
int index = size++;
vertices[index] = new Vertex(index, name);
}
public void addEdge(int start, int end) {
vertexList[start].add(vertices[end]);
vertexList[end].add(vertices[start]);
}
}
3. Search In Graph
3.1 Search Approaches
There are two common approaches to search a graph:
- Depth-First Search:
DFSis implemented with astack. - Breadth-First Search:
BFSis implemented with aqueue.
Depth-First Search(DFS)
- Rule 1: If possible, visit an adjacent unvisited vertex, mark it, and push it on the stack.
- Rule 2: If you can’t follow Rule 1, then, if possible, pop a vertex off the stack.
- Rule 3: If you can’t follow Rule 1 or Rule 2, you’re done.
Breadth-First Search(BFS)
- Rule 1: Visit the next unvisited vertex (if there is one) that’s adjacent to the current vertex, mark it, and insert it into the queue.
- Rule 2: If you can’t carry out Rule 1 because there are no more unvisited vertices, remove a vertex from the queue (if possible) and make it the current vertex.
- Rule 3: If you can’t carry out Rule 2 because the queue is empty, you’re done.
3.2 Search In Adjacency Matrix Graph
Given the above graph, the below dfs method returns [A, B, C, D, E] and the bfs method returns [A, B, E, C, D].
// dfs
private Stack<Vertex> stack = new Stack<Vertex>();
public String[] dfs() {
String[] res = new String[size];
vertices[0].visited = true;
int idx = 0;
res[idx++] = vertices[0].name;
stack.push(vertices[0]);
while (!stack.isEmpty()) {
int index = getUnvisitedVertex(stack.peek().index);
if (index == -1) { // no unvisited neighbor
stack.pop();
} else {
vertices[index].visited = true;
res[idx++] = vertices[index].name;
stack.push(vertices[index]);
}
}
// reset vertices
for (Vertex vertex : vertices) {
vertex.visited = false;
}
return res;
}
// bfs
private Queue<Vertex> queue = new LinkedList<Vertex>();
public String[] bfs() {
String[] res = new String[size];
vertices[0].visited = true;
int idx = 0;
res[idx++] = vertices[0].name;
queue.add(vertices[0]);
while (!queue.isEmpty() ) {
Vertex vertex = queue.poll();
int nextIdx = getUnvisitedVertex(vertex.index);
while (nextIdx != -1) {
vertices[nextIdx].visited = true;
res[idx++] = vertices[nextIdx].name;
queue.add(vertices[nextIdx]);
nextIdx = getUnvisitedVertex(vertex.index);
}
}
// reset vertices
for (Vertex vertex : vertices) {
vertex.visited = false;
}
return res;
}
private int getUnvisitedVertex(int index) {
for (int i = 0; i < size; i++) {
if (matrix[index][i] == 1 && vertices[i].visited == false) {
return i;
}
}
return -1;
}
3.3 Search In Adjacency List Graph
Given the above graph, the below dfs method returns [A, B, C, D, E] and the bfs method returns [A, B, E, C, D].
// dfs
private Stack<Vertex> stack = new Stack<Vertex>();
public String[] dfs() {
String[] res = new String[size];
vertices[0].visited = true;
int idx = 0;
res[idx++] = vertices[0].name;
stack.push(vertices[0]);
while (!stack.isEmpty()) {
int index = getUnvisitedVertex(stack.peek().index);
if (index == -1) { // no unvisited neighbor
stack.pop();
} else {
vertices[index].visited = true;
res[idx++] = vertices[index].name;
stack.push(vertices[index]);
}
}
// reset vertices
for (Vertex vertex : vertices) {
vertex.visited = false;
}
return res;
}
// bfs
private Queue<Vertex> queue = new LinkedList<Vertex>();
public String[] bfs() {
String[] res = new String[size];
vertices[0].visited = true;
int idx = 0;
res[idx++] = vertices[0].name;
queue.add(vertices[0]);
while (!queue.isEmpty() ) {
Vertex vertex = queue.poll();
int nextIdx = getUnvisitedVertex(vertex.index);
while (nextIdx != -1) {
vertices[nextIdx].visited = true;
res[idx++] = vertices[nextIdx].name;
queue.add(vertices[nextIdx]);
nextIdx = getUnvisitedVertex(vertex.index);
}
}
// reset vertices
for (Vertex vertex : vertices) {
vertex.visited = false;
}
return res;
}
private int getUnvisitedVertex(int index) {
for (int i = 0; i < vertexList[index].size(); i++) {
if (vertexList[index].get(i).visited == false) {
return vertexList[index].get(i).index;
}
}
return -1;
}
3.4 Bidirectional Search
Bidirectional search is used to find the shortest path between a source and destination node.
4. Node Graph
There is one additional way to represent graph. Graph can be represented with vertex(node) only. The edges are represented with neighbor nodes, stored as a property of the node.
4.1 Implementation
Node.
public class Node {
public String name;
public boolean visited;
public Node[] neighbors;
public Node(String name) {
this.name = name;
this.visited = false;
}
@Override
public String toString() {
return name;
}
}
Node Graph.
public class NodeGraph {
public Node[] nodes;
public NodeGraph(int size)
{
nodes = new Node[size];
}
public void addNeighbors(int index, Node[] neighbors) {
nodes[index].neighbors = neighbors;
}
}
4.2 Search
Both DFS and BFS approaches can be applied to Node Graph.
1) Traverse all nodes in graph with DFS.
// dfs, stack
public List<String> dfs(Node root) {
List<String> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Stack<Node> stack = new Stack<Node>();
root.visited = true;
ans.add(root.name);
stack.push(root);
while (!stack.isEmpty()) {
Node node = stack.peek();
Node neighbor = getUnvisitedNeighbor(node);
if (neighbor == null) {
stack.pop();
} else {
neighbor.visited = true;
ans.add(neighbor.name);
stack.push(neighbor);
}
}
return ans;
}
private Node getUnvisitedNeighbor(Node node) {
for (int i = 0; i < node.neighbors.length; i++) {
if (node.neighbors[i].visited == false) {
return node.neighbors[i];
}
}
return null;
}
For the DFS search, we can simplify the implementation without using stack. The dfs2 method calls itself recursively to generate the list.
// dfs, recursion
public void dfs2(Node root, List<String> list) {
if (root == null) {
return;
}
list.add(root.name);
root.visited = true;
for (Node neighbor : root.neighbors) {
if (neighbor.visited == false) {
dfs2(neighbor, list);
}
}
}
2) Traverse all nodes in graph with BFS.
public List<String> bfs(Node root) {
List<String> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Queue<Node> queue = new LinkedList<Node>();
root.visited = true;
ans.add(root.name);
queue.offer(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
for (Node neighbor : node.neighbors) {
if (neighbor.visited == false) {
neighbor.visited = true;
ans.add(neighbor.name);
queue.offer(neighbor);
}
}
}
return ans;
}