1132. Data Structure - HeapMax Heap and Min Heap
Implement heap with array.
1. Heap
1.1 Definition of Heap
A heap is a binary tree with these characteristics:
- It’s complete. This means it’s completely filled in, reading from left to right across each row, although the last row need not be full.
- It’s (usually) implemented as an array. Binary trees can be stored in arrays, rather than using references to connect the nodes.
- Each node in a heap satisfies the
heap condition, which states that every node’s key is larger/smaller than the keys of its children.
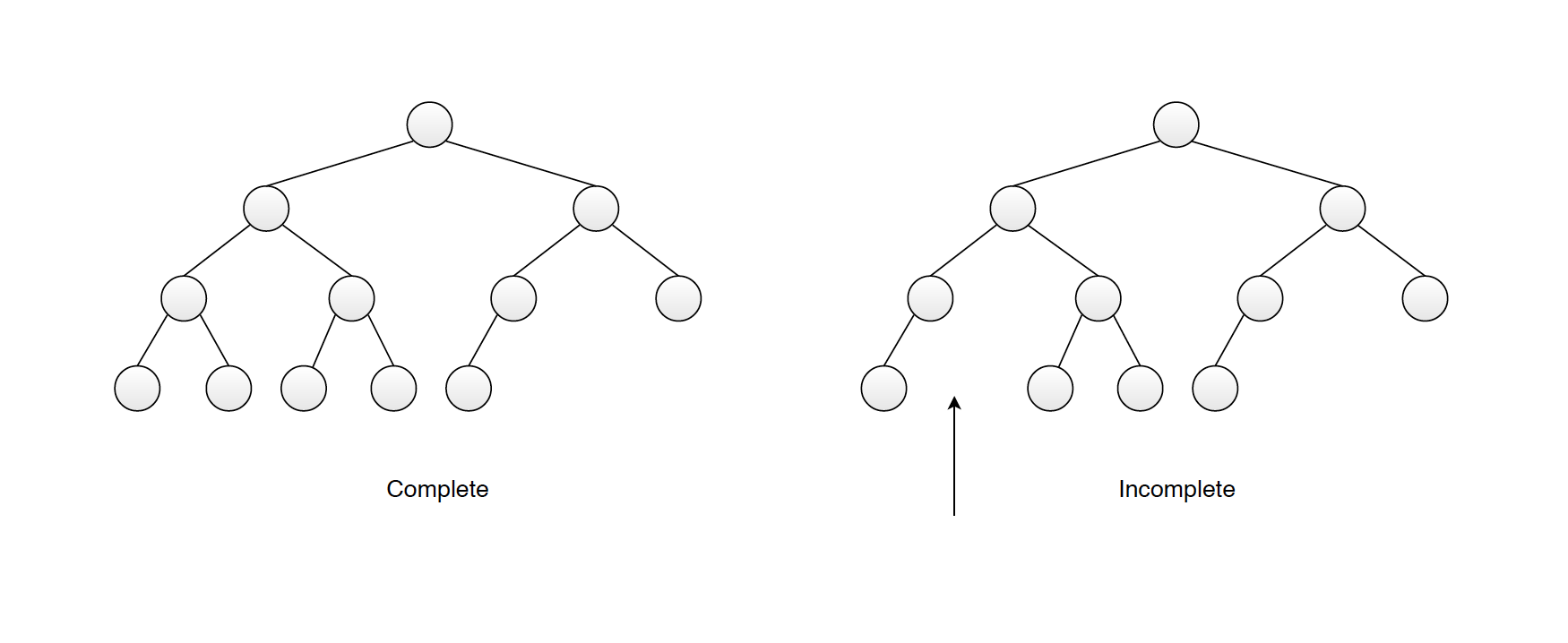
1.2 Types of Heap
- Max Heap - The value of each node is less than the value of its parent, with the maximum-value element at the root.
- Min Heap - The value of each node is greater than the value of its parent, with the minimum-value element at the root.
1.3 Common Operations on Heap
- Insertion - Insert a new value to heap.
- Removal - Remove and return the root.
- Get - Get the value of root.
1.4 Time Complexity
- Insertion - $O(\log{}n)$
- Removal - $O(\log{}n)$
- Get - $O(1)$
1.5 Efficiency of Heap Operations
A heap is a special kind of binary tree, the number of levels L in a binary tree equals $\log_{2}(N+1)$, where N is the number of nodes. The bubble up and bubble down routines cycle through their loops L-1 times, so the first takes time proportional to $\log_{2}N$, and the second somewhat more because of the extra comparison. Thus, the heap operations we’ve talked about here all operate in $O(\log{}N)$ time.
1.6 Elements Sequence
If you remove a node and then insert the same node, the result is not necessarily the restoration of the original heap. A given set of nodes can be arranged in many valid heaps, depending on the order in which nodes are inserted.
2. Heap Implementation
2.1 Array Heap
Heap can be implemented with array. A heap is a complete binary tree implies that there are no “holes” in the
array used to represent it. The traversal method use to achieve array representation is Level Order.
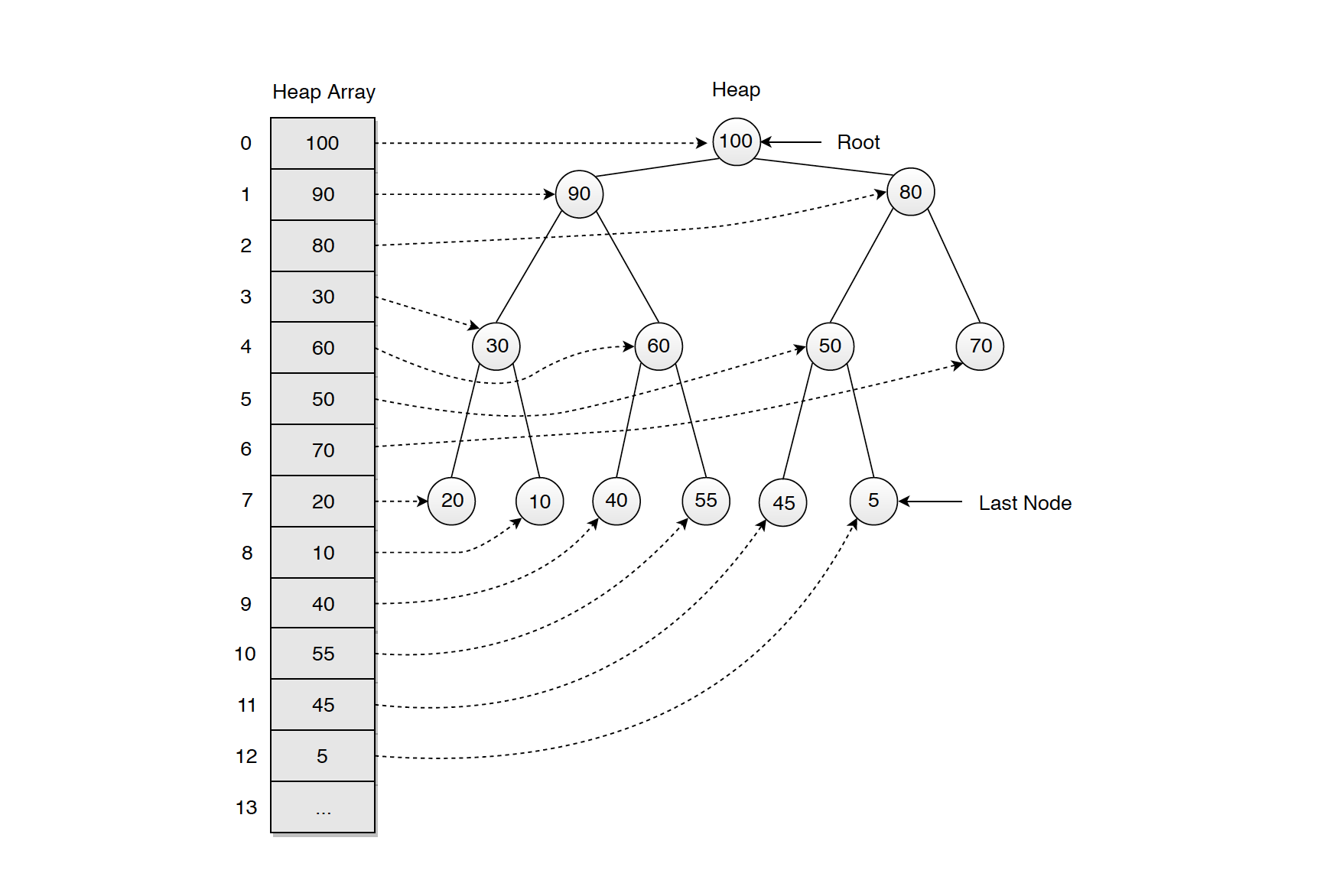
2.2 Index Relationship
For a node at index i in the array,
- Its parent is (i - 1) / 2.
- Its left child is 2 * i + 1.
- Its right child is 2 * i + 2.
3. Max Heap
A max-heap is a complete binary tree where each node is larger than its children. The root, therefore, is the maximum element in the heap.
3.1 Insertion
Insertion means add new element to the heap. Initially, the new element is placed in the first open position at the end of the array. Insertion increases the array size by one. Here are the steps for adding the new element to max heap:
- 1) Add new node to bottom, rightmost.
- 2) Compare the value of this node with its parent. If value of parent is less than child, then swap them.
- 3) Repeat step 2) to bubble up this new node to maintain the heap condition if possible; otherwise, stop.
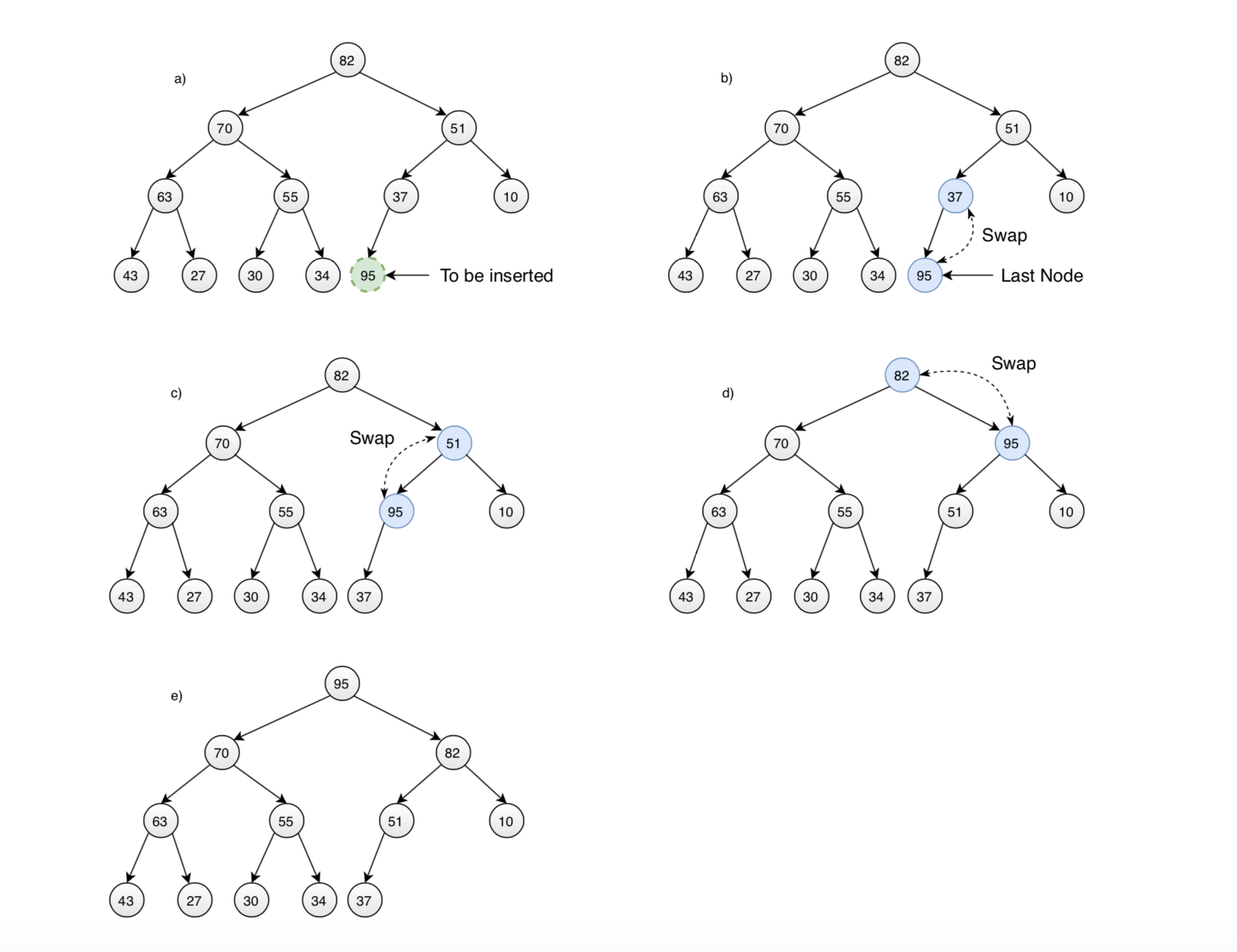
3.2 Removal
Removal means removing the node with the maximum key. This node is always the root. Removing decreases the array size by one. Here are the steps for removing the maximum node:
- 1) Remove the root node.
- 2) Move the last element(bottom, rightmost) to root.
- 3) Compare the value of this child with its parent. If value of parent is less than child, then swap them.
- 4) Repeat step 3) to bubble down this node to maintain the heap condition if possible; otherwise, stop.
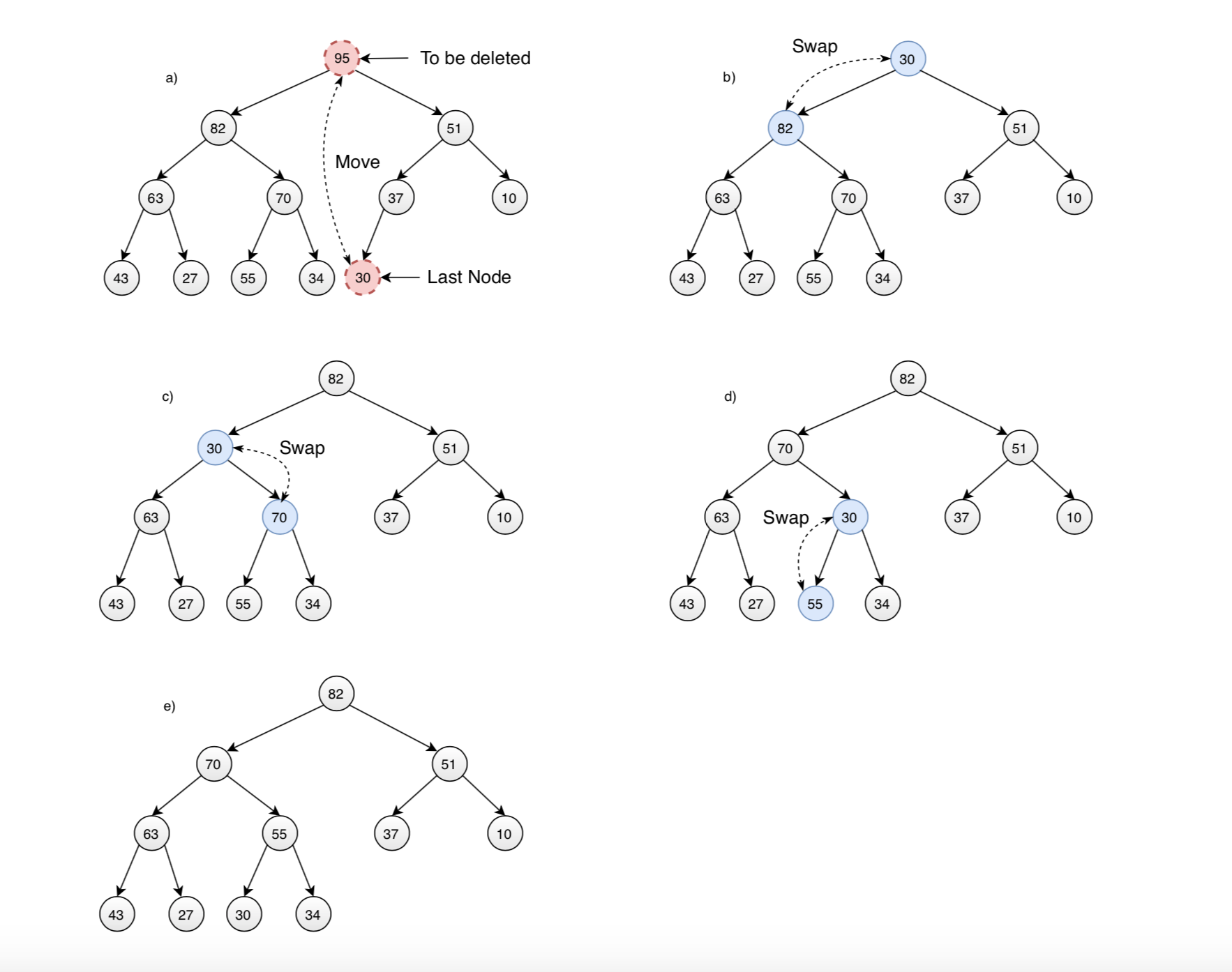
3.3 Implementing MaxHeap
The following code is the implementation of max heap with type integer.
public class MaxHeap {
private int capacity = 10;
protected Integer[] array;
protected int size;
public MaxHeap () {
array = new Integer[capacity];
size = 0;
}
public MaxHeap (int capacity) {
this.capacity = capacity;
array = new Integer[capacity];
size = 0;
}
// add new element into heap
public void add(int value) {
if (size >= array.length - 1) {
array = this.resize();
}
// place element into heap at bottom (right most)
array[size] = value;
size++;
bubbleUp();
}
// bubble up the last node with it's parent until they are in the order of max heap
protected void bubbleUp() {
int index = this.size - 1; // last node (right most)
while (hasParent(index) && (parent(index) < array[index])) {
// parent and child are out of order; swap them
swap(index, parentIndex(index));
index = parentIndex(index);
}
}
// remove and return the maximum element in the heap
public int remove() {
if (this.isEmpty()) {
throw new IllegalStateException();
}
// get the root, which is the maximum value
int result = peek();
// move the last leaf to root
array[0] = array[size - 1];
array[size - 1] = null;
size--;
bubbleDown();
return result;
}
// bubble down the new root to proper position to maintain the order of max heap
protected void bubbleDown() {
// root
int index = 0;
// heap is complete tree, so it's safe to check left child first
while (hasLeftChild(index)) {
int biggerChild = leftIndex(index);
// find the smaller child
if (hasRightChild(index)
&& array[leftIndex(index)] < (array[rightIndex(index)])) {
biggerChild = rightIndex(index);
}
if (array[index] > array[biggerChild]) {
break;
} else {
// parent and child are out of order; swap them
swap(index, biggerChild);
index = biggerChild;
}
}
}
// get the root without removing it from heap
public int peek() {
if (this.isEmpty()) {
throw new IllegalStateException();
}
return array[0];
}
public boolean isEmpty() {
return size == 0;
}
public int size() {
return size;
}
protected boolean hasParent(int i) {
return i > 0;
}
protected int leftIndex(int i) {
return 2 * i + 1;
}
protected int rightIndex(int i) {
return 2 * i + 2;
}
protected boolean hasLeftChild(int i) {
return leftIndex(i) <= size - 1;
}
protected boolean hasRightChild(int i) {
return rightIndex(i) <= size - 1;
}
protected int parent(int i) {
return array[parentIndex(i)];
}
protected int parentIndex(int i) {
return (i - 1) / 2;
}
protected Integer[] resize() {
return Arrays.copyOf(array, array.length * 2);
}
protected void swap(int index1, int index2) {
int tmp = array[index1];
array[index1] = array[index2];
array[index2] = tmp;
}
}
4. Min Heap
A min-heap is a complete binary tree where each node is smaller than its children. The root, therefore, is the minimum element in the heap.
4.1 Implementing MinHeap
The following code is the implementation of max heap with type integer. The only difference with max heap is the comparison.
public class MinHeap {
private int capacity = 10;
protected Integer[] array;
protected int size;
public MinHeap () {
array = new Integer[capacity];
size = 0;
}
public MinHeap (int capacity) {
this.capacity = capacity;
array = new Integer[capacity];
size = 0;
}
// add new element into heap
public void add(int value) {
if (size >= array.length - 1) {
array = this.resize();
}
// place element into heap at bottom (right most)
array[size] = value;
size++;
bubbleUp();
}
// bubble up the last node with it's parent until they are in the order of max heap
protected void bubbleUp() {
int index = this.size - 1; // last node (right most)
while (hasParent(index) && (parent(index) > array[index])) {
// parent and child are out of order; swap them
swap(index, parentIndex(index));
index = parentIndex(index);
}
}
// remove and return the maximum element in the heap
public int remove() {
if (this.isEmpty()) {
throw new IllegalStateException();
}
// get the root, which is the maximum value
int result = peek();
// move the last leaf to root
array[0] = array[size - 1];
array[size - 1] = null;
size--;
bubbleDown();
return result;
}
// bubble down the new root to proper position to maintain the order of max heap
protected void bubbleDown() {
// root
int index = 0;
// heap is complete tree, so it's safe to check left child first
while (hasLeftChild(index)) {
int biggerChild = leftIndex(index);
// find the smaller child
if (hasRightChild(index)
&& array[leftIndex(index)] > (array[rightIndex(index)])) {
biggerChild = rightIndex(index);
}
if (array[index] < array[biggerChild]) {
break;
} else {
// parent and child are out of order; swap them
swap(index, biggerChild);
index = biggerChild;
}
}
}
// get the root without removing it from heap
public int peek() {
if (this.isEmpty()) {
throw new IllegalStateException();
}
return array[0];
}
public boolean isEmpty() {
return size == 0;
}
public int size() {
return size;
}
protected boolean hasParent(int i) {
return i > 0;
}
protected int leftIndex(int i) {
return 2 * i + 1;
}
protected int rightIndex(int i) {
return 2 * i + 2;
}
protected boolean hasLeftChild(int i) {
return leftIndex(i) <= size - 1;
}
protected boolean hasRightChild(int i) {
return rightIndex(i) <= size - 1;
}
protected int parent(int i) {
return array[parentIndex(i)];
}
protected int parentIndex(int i) {
return (i - 1) / 2;
}
protected Integer[] resize() {
return Arrays.copyOf(array, array.length * 2);
}
protected void swap(int index1, int index2) {
int tmp = array[index1];
array[index1] = array[index2];
array[index2] = tmp;
}
}
5. Heap Sort
Construct a heap with all numbers, and delete root one by one to get the sorted list.
6. Priority Queue
Priority queues are useful for any application that involves processing elements based on some priority.
Priority Queue vs Heap
A priority queue can be implemented using many of the data structures(Array, Linked List, or Binary Search Tree). However, those data structures do not provide the most efficient operations. To make all of the operations very efficient, we’ll use a new data structure called a heap.
Priority Queue vs TreeMap
- PriorityQueue Allows Duplicate(i.e with same priority) while TreeMap doesn’t.
- Complexity of PriorityQueue is O(n)(when is increases its size), while that of TreeMap is O(logn)(as it is based on Red Black Tree)
- PriorityQueue is based on Array while in TreeMap nodes are linked to each other, so contains method of PriorityQueue would take O(n) time while TreeMap would take O(logn) time.
6.1 Common Operations on Priority Queue
- Add - Insert a new value to priority queue.
- Poll - Remove and return the maximum/minimum.
- Peek - Get the maximum/minimum.
6.2 Time Complexity
- Add - $O(\log{}n)$
- Poll - $O(\log{}n)$
- Peek - $O(1)$
6.3 Max Priority Queue
public class PriorityQueueMax {
private MaxHeap heap;
public PriorityQueueMax() {
heap = new MaxHeap();
}
public PriorityQueueMax(int capacity) {
heap = new MaxHeap(capacity);
}
public void add(int val) {
heap.add(val);
}
public int poll() {
return heap.remove();
}
public int peek() {
return heap.peek();
}
public boolean isEmpty() {
return heap.size == 0;
}
public int size() {
return heap.size;
}
}
6.4 Min Priority Queue
public class PriorityQueueMin {
private MinHeap heap;
public PriorityQueueMin() {
heap = new MinHeap();
}
public PriorityQueueMin(int capacity) {
heap = new MinHeap(capacity);
}
public void add(int val) {
heap.add(val);
}
public int poll() {
return heap.remove();
}
public int peek() {
return heap.peek();
}
public boolean isEmpty() {
return heap.size == 0;
}
public int size() {
return heap.size;
}
}
7. Classic Problems
- LeetCode 295 - Find Median from Data Stream
- LeetCode 42 - Trapping Rain Water
- LintCode 364 - Trapping Rain Water II
- LeetCode 218 - The Skyline Problem
- LeetCode 480 - Sliding Window Median