1117. Data Structure - LFU CacheLFU and Cache
Implement Least Frequently Used(LFU) cache.
1. LFU
1.1 LFU Cache Algorithm
Least Frequently Used(LFU) cache algorithm uses a counter to keep track of how often an entry is accessed. With the LFU cache algorithm, the entry with the lowest count is removed first. This method isn’t used that often, as it does not account for an item that had an initially high access rate and then was not accessed for a long time.
1.2 How It Works?
The LFU cache provides two methods: add and get.
- add(key, value) - Add the value into cache if it is not already present. When the cache reached its capacity, it should invalidate the least frequently used item before inserting a new item. If there is a tie (i.e., two or more keys that have the same frequency), the least recently used key would be evicted.
- get(key) - If the key doesn’t exist in the cache, return the minimum value of Integer. Otherwise, return the value of the key and move this element to the proper position of the cache.
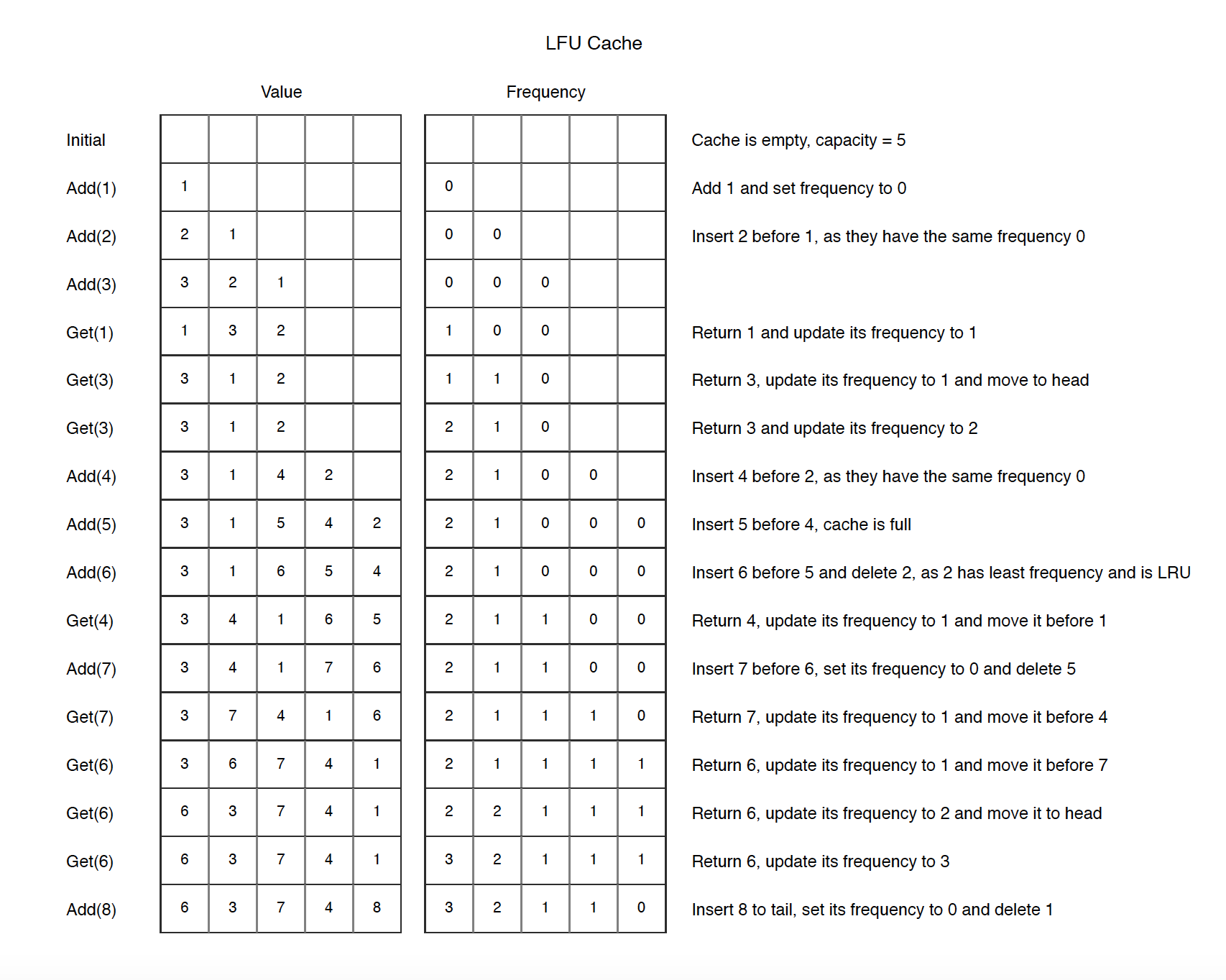
The following diagram illustrates how LFU works.
2. Implementation
2.1 Data Structure
LFU algorithm can be easily implemented with HashMap and Doubly Linked List.
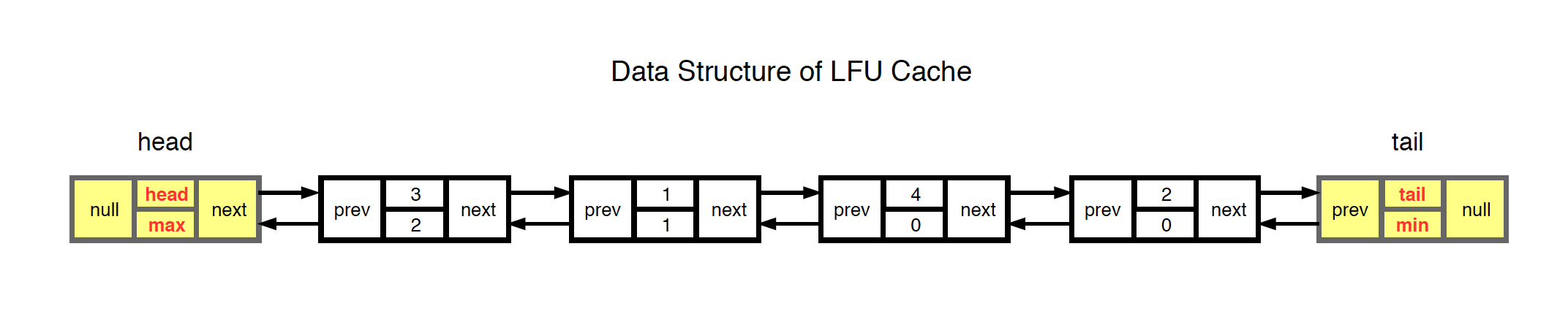
- The head and tail nodes don’t store any data. They are created just for conveniently manipulating the linked list.
- Nodes between the head and tail nodes are used to store data, each node for one value. Every node has two pointers, pointing to the previous and the next nodes. Each node has two attributes, one is the value and another is the count of this node.
- Nodes near the tail are least frequently accessed. They will be removed if cache reaches to its capacity.
- Nodes in LFU are sorted by frequency(count).
2.2 Operations On LFU
1) Initialization
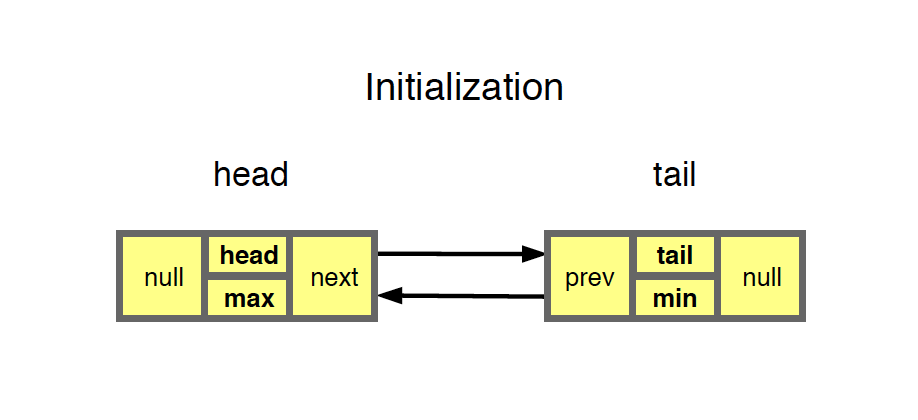
- Only two dummy nodes, head and tail.
- Notice that there is another HashMap which stores the value-node pair.
2) Add (Cache is not full and maximum frequency = 0)
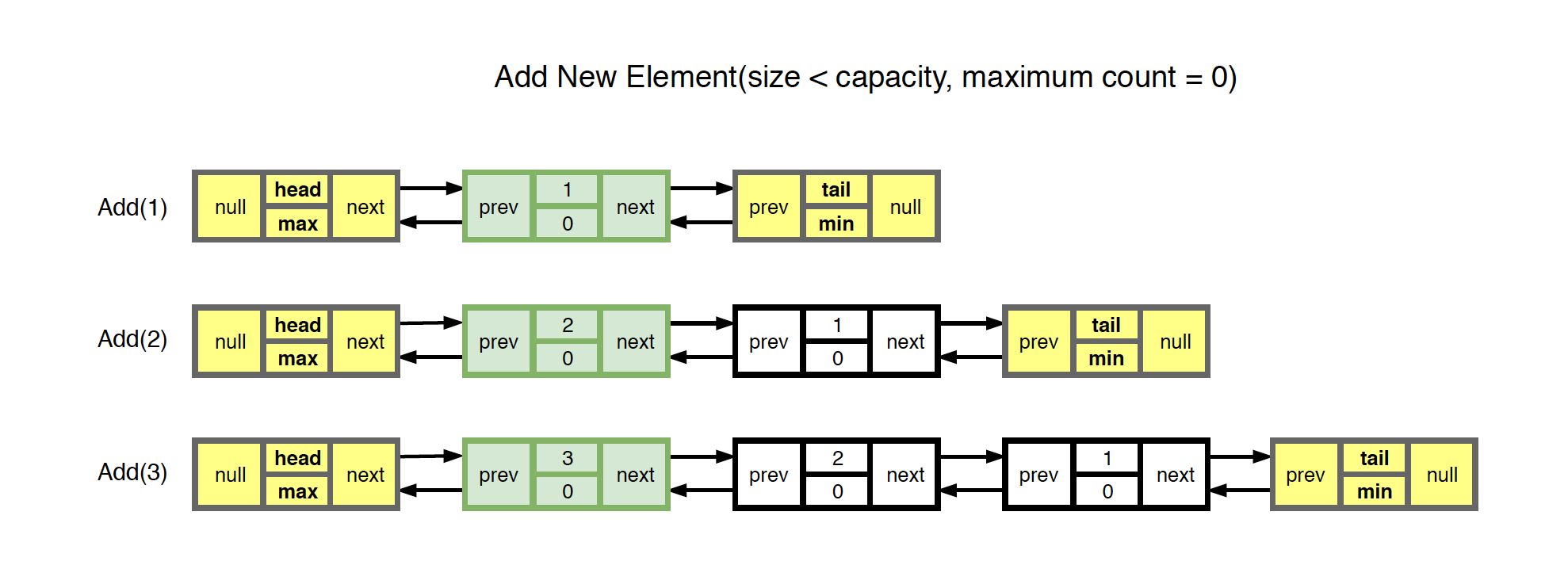
- Create new node for the given value and insert it to the head of the linked list.
- Add the new node to HashMap with the given value as key.
- Size is increased by one.
3) Add (Cache is not full and maximum frequency > 0)
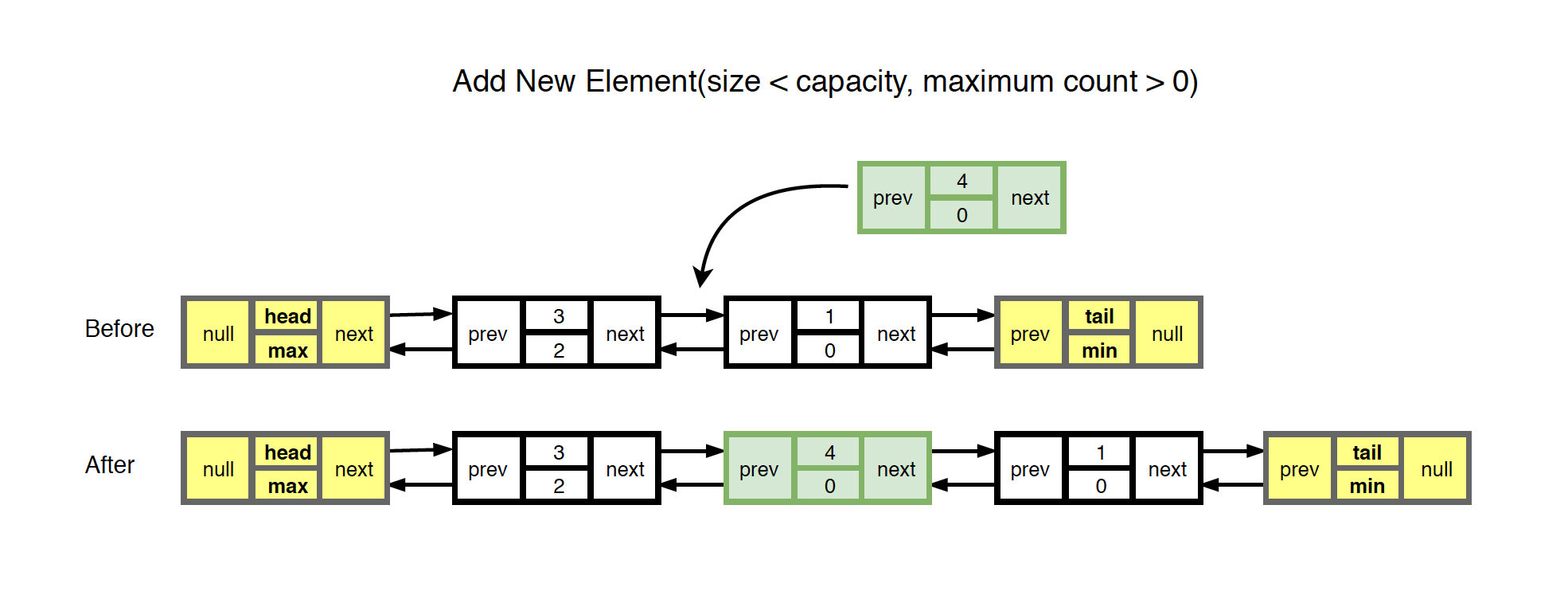
- Create new node for the given value and insert it before the node which has the same frequency or to the tail.
- Add the new node to HashMap with the given value as key.
- Size is increased by one.
4) Add (Cache is full)
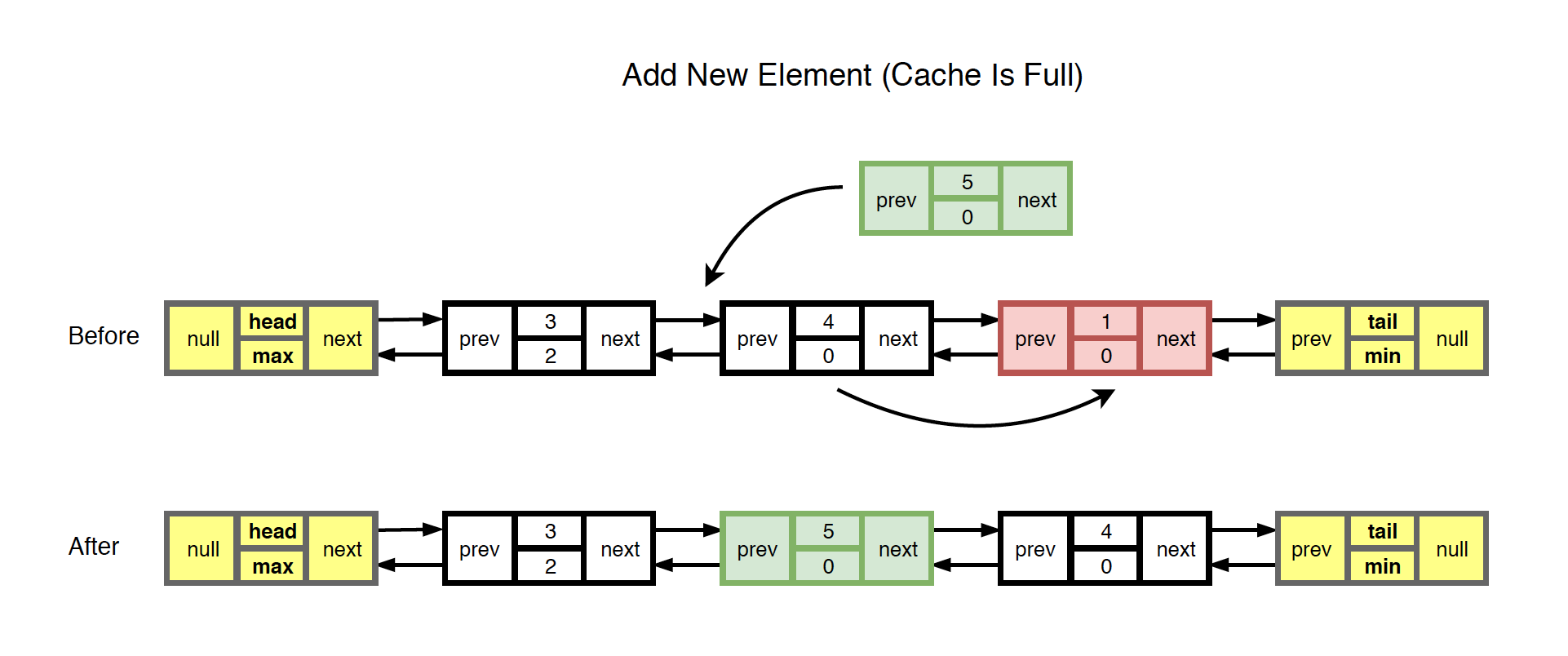
- Remove the last element(The one tail.prev is pointing) from the list.
- Create new node for the given value and insert it before the node which has the same frequency or to the tail.
- Add the new node to HashMap with the given value as key.
- Size remains unchanged.
5) Get
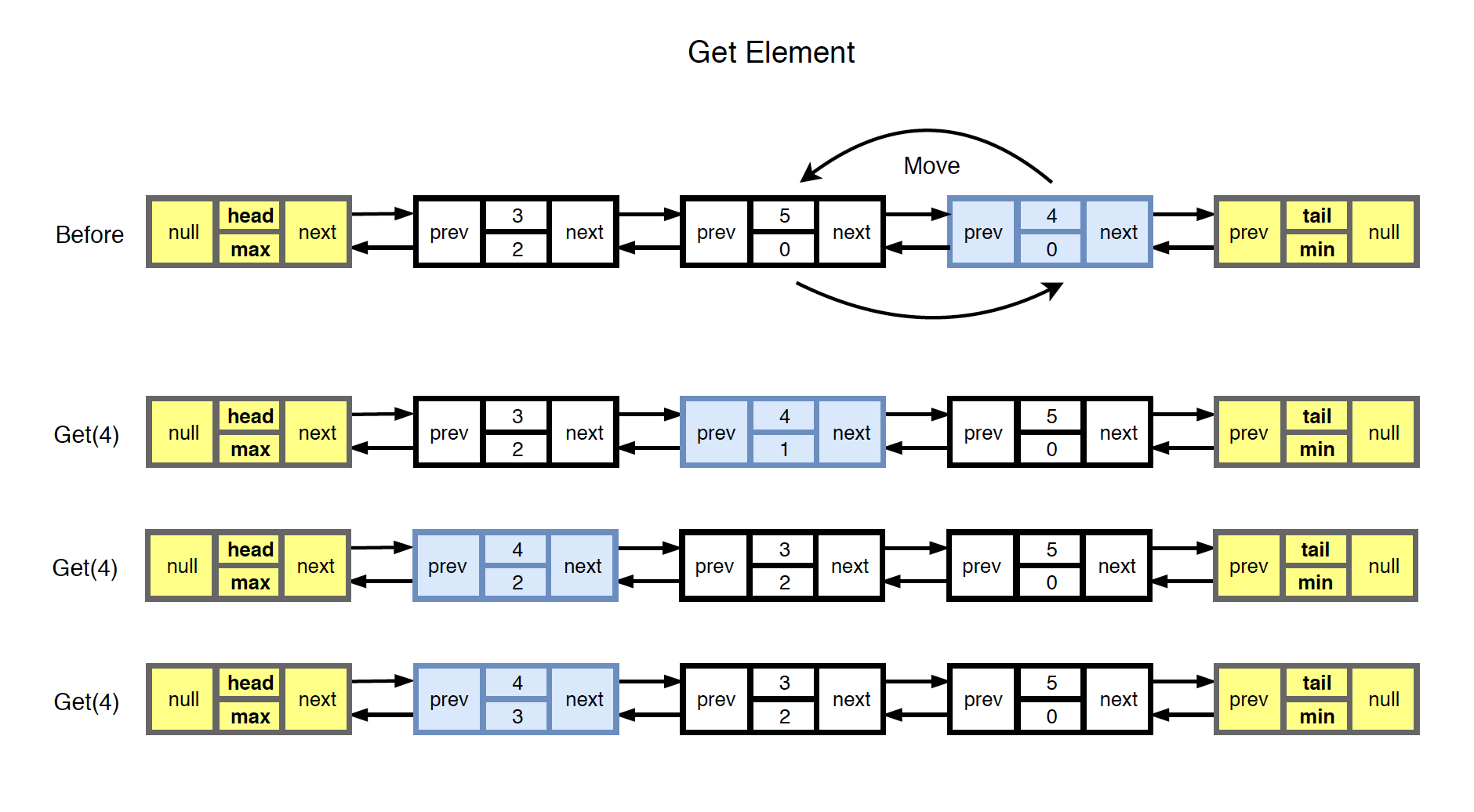
- Find the given value in HashMap.
- Increase the frequency of this node by one. Move it to proper position of the linked list.
- Return the value.
2.3 Built With Custom Node
The following code is the implementation of LFU based on custom nodes. The node is defined as follows.
public class Node {
public int value;
public int count;
public Node prev;
public Node next;
public Node(int value, int count) {
this.value = value;
this.count = count;
this.prev = null;
this.next = null;
}
}
Following is the LFU class which implements the add() and get() methods.
public class LFU {
private int capacity;
private HashMap<Integer, Node> map; // key, node
private Node head; // The most frequently accessed element
private Node tail; // The least frequently used element
private final int MAX = Integer.MAX_VALUE;
private final int MIN = Integer.MIN_VALUE;
public LFU(int capacity) {
this.capacity = capacity;
this.map = new HashMap<Integer, Node>();
this.head = new Node(this.MAX, this.MAX);
this.tail = new Node(this.MIN, this.MIN);
head.next = tail;
tail.prev = head;
}
public void add(int key, int value) {
if (map.containsKey(key)) {
return;
}
if (map.size() == capacity) {
map.remove(tail.prev.value);
tail.prev = tail.prev.prev;
tail.prev.next = tail;
}
Node newNode = new Node(key, 0);
map.put(key, newNode);
// move new node to proper position
move(newNode);
}
public int get(int key) {
if (!map.containsKey(key)) {
return this.MIN;
}
// remove current
Node current = map.get(key);
current.prev.next = current.next;
current.next.prev = current.prev;
current.count++; // increment before move
// move current node to proper position
move(current);
return map.get(key).value;
}
private void move(Node node) {
Node curr = head;
while (curr != null) {
if (curr.count > node.count) {
curr = curr.next;
} else {
node.prev = curr.prev;
node.next = curr;
node.next.prev = node;
node.prev.next = node;
break;
}
}
}
}
Time complexity:
- add() - $O(n)$
- get() - $O(n)$
Space complexity:
- $O(n)$, 2*N, N is the number of nodes
2.4 Testing
Create an instance of LFU class and call add() and get() methods. The changes of the value and frequency list are described in the inline comments.
LFU lfu = new LFU(5); //capacity = 5
lfu.add(1,1); // value = [1], frequency = [0]
lfu.add(2,2); // value = [2,1], frequency = [0,0]
lfu.add(3,3); // value = [3,2,1], frequency = [0,0,0]
lfu.get(1); // value = [1,3,2], frequency = [1,0,0], return 1
lfu.get(3); // value = [3,1,2], frequency = [1,1,0], return 3
lfu.get(3); // value = [3,1,2], frequency = [2,1,0], return 3
lfu.add(4,4); // value = [3,1,4,2], frequency = [2,1,0,0]
lfu.add(5,5); // value = [3,1,5,4,2], frequency = [2,1,0,0,0], cache is full
lfu.add(6,6); // value = [3,1,6,5,4], frequency = [2,1,0,0,0], last element 2 is removed
lfu.get(4); // value = [3,4,1,6,5], frequency = [2,1,1,0,0], return 4
lfu.add(7,7); // value = [3,4,1,7,6], frequency = [2,1,1,0,0], last element 5 is removed
lfu.get(7); // value = [3,7,4,1,6], frequency = [2,1,1,1,0], return 7
lfu.get(6); // value = [3,6,7,4,1], frequency = [2,1,1,1,1], return 6
lfu.get(6); // value = [6,3,7,4,1], frequency = [2,2,1,1,1], return 6
lfu.get(6); // value = [6,3,7,4,1], frequency = [3,2,1,1,1], return 6
lfu.add(8,8); // value = [6,3,7,4,8], frequency = [3,2,1,1,0], last element 1 is removed
3. Optimization
3.1 Implementation With Custom Node
Time complexity can be $O(n)$ in worst case. This is because in the ‘move’ method, we may have to traverse all the node to find the proper position to insert the given node.
private void move(Node node) {
Node curr = head;
while (curr != null) {
if (curr.count > node.count) {
curr = curr.next;
} else {
node.prev = curr.prev;
node.next = curr;
node.next.prev = node;
node.prev.next = node;
break;
}
}
}
3.2 Potential Improvement
To improve the performance, we have two destinations, $O(\log{}n)$ or $O(1)$. Use hashmap.
public class LFUHashMap {
HashMap<Integer, Integer> values; // key, value
HashMap<Integer, Integer> counts; // key, count
HashMap<Integer, LinkedHashSet<Integer>> lists; // count, list->keys
int cap;
int min = -1;
public LFUHashMap(int capacity) {
cap = capacity;
values = new HashMap<>();
counts = new HashMap<>();
lists = new HashMap<>();
lists.put(0, new LinkedHashSet<>());
}
public void add(int key, int value) {
if (cap <= 0) {
return;
}
if (values.containsKey(key)) {
values.put(key, value);
get(key); // trigger the reorder
return;
}
if (values.size() >= cap) {
int evict = lists.get(min).iterator().next();
lists.get(min).remove(evict);
values.remove(evict);
counts.remove(evict);
}
values.put(key, value);
counts.put(key, 0);
min = 0;
lists.get(0).add(key);
}
public int get(int key) {
if (!values.containsKey(key)) {
return -1;
}
int count = counts.get(key);
counts.put(key, count + 1);
lists.get(count).remove(key);
if (count == min && lists.get(count).size() == 0) {
min++;
}
if (!lists.containsKey(count+1)) {
lists.put(count + 1, new LinkedHashSet<>());
}
lists.get(count + 1).add(key);
return values.get(key);
}
}
Time complexity:
- add() - $O(1)$
- get() - $O(1)$
Space complexity:
- $O(n)$, 3*N, N is the number of keys