1112. Data Structure - StackStack and LIFO
Implement stack with linked list and array.
1. Stack
1.1 Real-life Example
Stack is just like a pile of plates kept on top of each other. You can only take out a plate from the top and put a plate on top of the other plates.

Think about the things you can do with such a pile of plates.
- Put a new plate on top
- Remove the top plate
If you want the plate at the bottom, you have to first remove all the plates on top.
1.2 Stack in Programming Terms
Stack is an abstract data type that serves as a collection of elements, with two principal operations:
push: add an element to the collectionpop: remove the most recently added element
Stack follows the LIFO(Last-in, first-out) rule. The last item that was placed is the first item to go out.
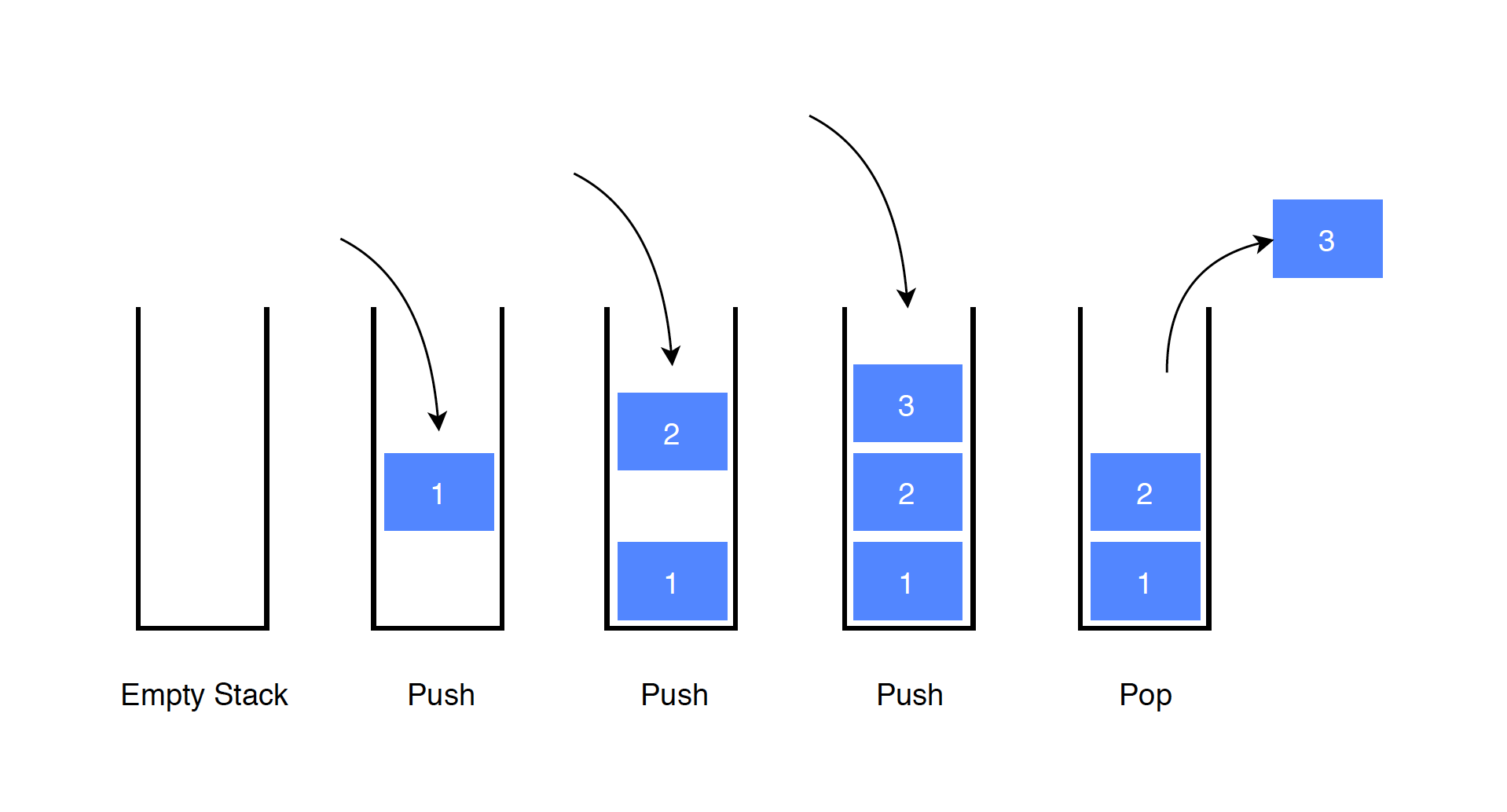
1.3 Common Operations on Stack
- push(item): Add an item to the top of the stack.
- pop(): Remove the top item from the stack.
- peek(): Return the top of the stack.
- isEmpty(): Return true if the stack is empty.
1.4 Time Complexity
- push: $O(1)$
- pop: $O(1)$
- peek: $O(1)$
2. Implementation
Four ways to implement stack.
- Linked List
- Array
- Circular Array(No need)
- Queues
2.1 Using Linked List
The head of the Linked List keeps the latest added item, which is the top of stack.
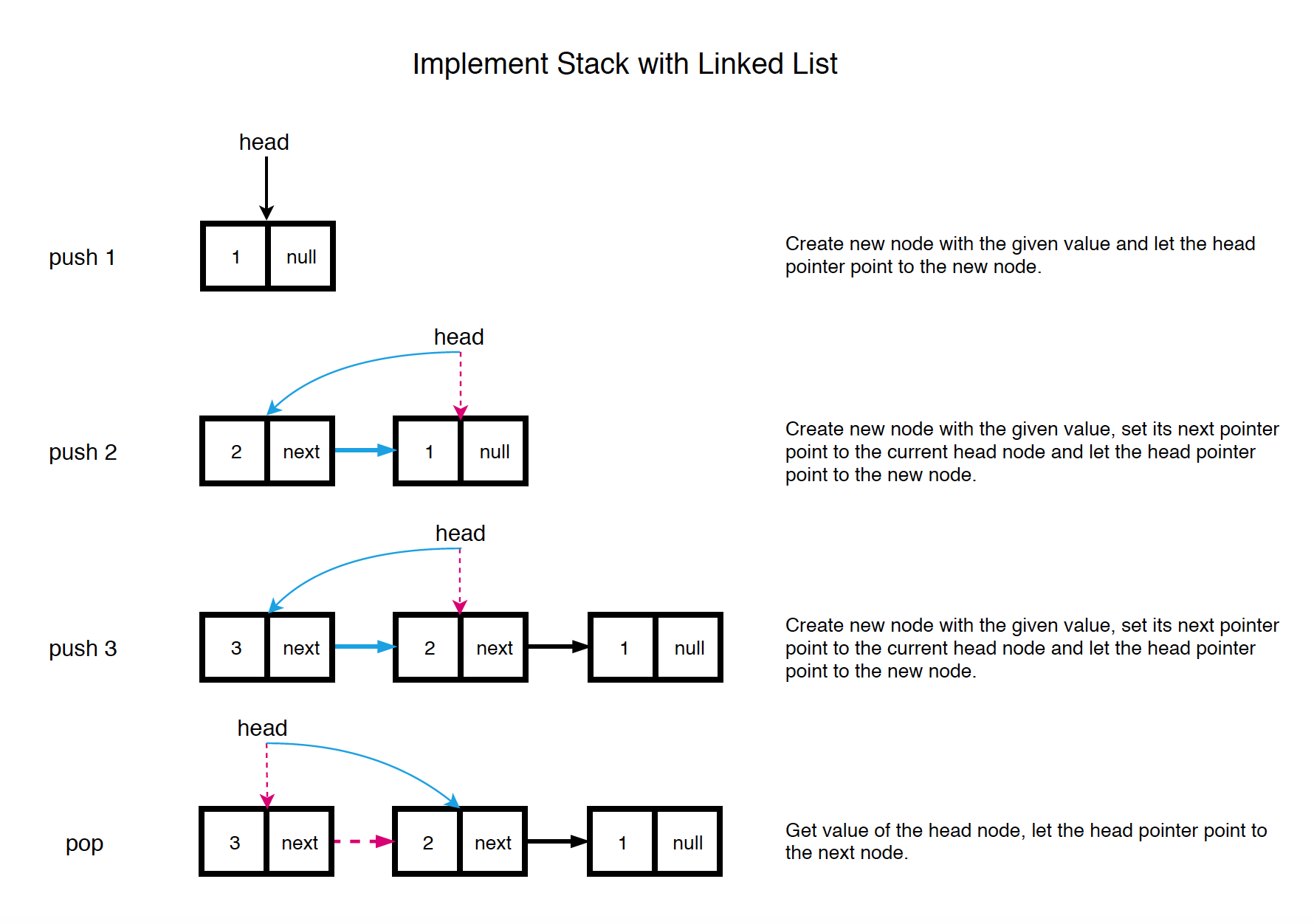
- push: Create new node with the given value, set its next pointer point to the current head node and let the head pointer point to the new node.
- pop: Get value of the head node, let the head pointer point to the next node.
See the implementation below. First, define the list node as follows.
public class ListNode {
public int val;
public ListNode next;
public ListNode(int val) {
this.val = val;
this.next = null;
}
}
Then, create the stack with list nodes.
public class LinkedListStack {
private ListNode head; // the head node
public LinkedListStack() {
head = null;
}
// Add item to the list, let head point to the new node
public void push(int value) {
ListNode oldHead = head;
head = new ListNode(value);
head.next = oldHead;
}
// Remove the head item from the list and return its value
public int pop() throws Exception {
if (head == null) {
throw new Exception();
}
int value = head.val;
head = head.next;
return value;
}
// Get the value of the head item
public int peek() throws Exception {
if (head == null) {
throw new Exception();
}
return head.val;
}
// Return whether the list is empty
public boolean isEmpty() {
return head == null;
}
}
2.2 Using Array
The top pointer is always pointing to the latest added item, which is the top of stack.
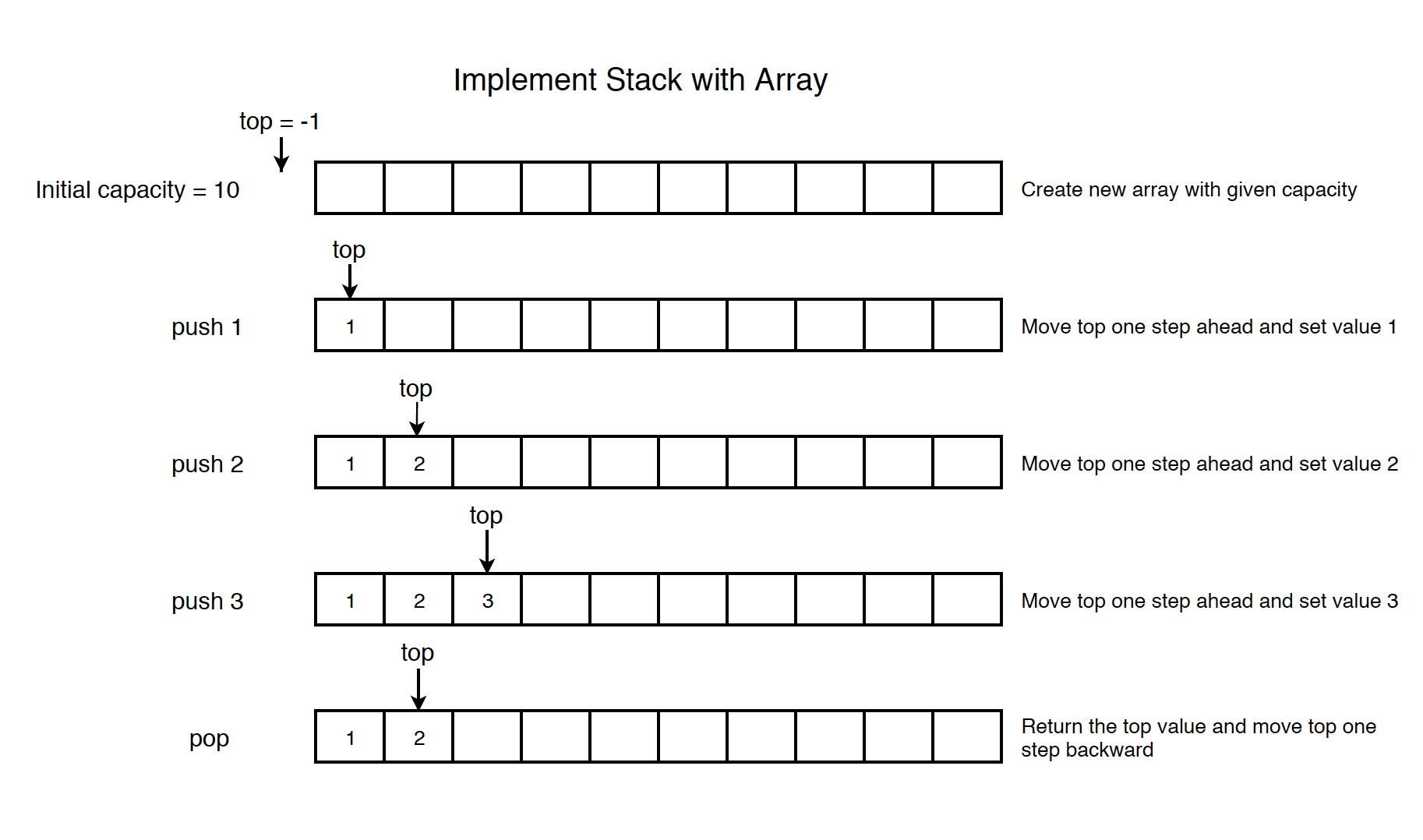
- push: Move top pointer one step ahead and put the given value.
- pop: Return the top value and move top pointer one step backward.
See the implementation below.
public class ArrayStack {
private int top;
private int[] arr;
public ArrayStack(int capacity) {
arr = new int[capacity];
top = -1;
}
// Add new element to the end of the array
public void push(int value) {
arr[++top] = value;
}
// Remove the last element from the array and return its value
public int pop() throws Exception {
if (top < 0) {
throw new Exception();
}
int value = arr[top];
top--;
return value;
}
// Get the top element
public int peek() throws Exception {
if (top < 0) {
throw new Exception();
}
return arr[top];
}
// Return whether the stack is empty
public boolean isEmpty() {
return top < 0;
}
}
2.3 Using Circular Array
No need to use circular array to implement stack. As you see how we implement stack with array, no space is wasted after pop operation. While in queue(implemented with array), empty cell appears after poll method gets called.
2.4 Using Two Queues
Time complexity: push: O(1), pop: O(n), peek: O(1)
import java.util.LinkedList;
import java.util.Queue;
public class QueueStack {
Queue<Integer> queue1; // Q1 always has all of the elements
Queue<Integer> queue2; // Q2 always be empty after pop
int top = 0;
// Initialize your data structure here.
public QueueStack() {
queue1 = new LinkedList<Integer>();
queue2 = new LinkedList<Integer>();
}
// Push element x onto stack.
public void push(int x) {
queue1.offer(x);
top = x;
}
// Removes the element on top of the stack and returns that element.
public int pop() {
while (queue1.size() > 1) {
top = queue1.poll();
queue2.offer(top);
}
int res = queue1.poll();
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
return res;
}
// Get the top element.
public int top() {
return top;
}
// Returns whether the stack is empty.
public boolean empty() {
return queue1.isEmpty();
}
}
2.5 Using One Queue
Time complexity: push: O(n), pop: O(1), peek: O(1)
import java.util.LinkedList;
import java.util.Queue;
public class QueueStack {
private LinkedList<Integer> queue;
/** Initialize your data structure here. */
public QueueStack() {
queue = new LinkedList<>();
}
/** Push element x onto stack. */
public void push(int x) {
queue.add(x);
int sz = queue.size();
while (sz > 1) {
queue.add(queue.remove());
sz--;
}
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue.remove();
}
/** Get the top element. */
public int top() {
return queue.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue.isEmpty();
}
}
3. Implementing Sorting Algorithms with Stack
3.1 Insertion Sort with Stack
If we call the sort method with array {2,4,5,7,1,2,3,6}, it will return a stack, which contains {1,2,2,3,4,5,6,7}, 7 is at top.
import java.util.Stack;
public class StackInsertionSort {
// Insertion Sort
public Stack<Integer> sort(int[] nums) {
if (nums == null || nums.length == 0) {
return null;
}
// initialize stack1
Stack<Integer> stack = new Stack<Integer>();
for (int i = 0; i < nums.length; i++) {
stack.push(nums[i]);
}
// stack2 contains the sorted items
Stack<Integer> stack2 = new Stack<Integer>();
while (!stack.isEmpty()) {
int top = stack.pop();
if (stack2.isEmpty()) {
stack2.push(top);
continue;
}
while (!stack2.isEmpty() && stack2.peek() > top) {
stack.push(stack2.pop());
}
stack2.push(top);
}
return stack2;
}
}
3.2 Merge Sort with Stack
If we call the sort method with array {2,4,5,7,1,2,3,6}, it will return a stack, which contains {1,2,2,3,4,5,6,7}, 7 is at top.
import java.util.Stack;
public class StackMergeSort {
// Merge Sort
public Stack<Integer> sort(int[] nums) {
if (nums == null || nums.length == 0) {
return null;
}
// initialize stack1
Stack<int[]> stack = new Stack<int[]>();
for (int i = 0; i < nums.length; i++) {
// convert number to number array
stack.push(new int[]{nums[i]});
}
// stack2 contains the sorted sub arrays
Stack<int[]> stack2 = new Stack<int[]>();
while (stack.size() > 1) {
while (stack.size() > 1) {
int[] r = stack.pop();
int[] l = stack.pop();
int[] merged = merge(l, r);
stack2.push(merged);
}
while (stack2.size() > 1) {
int[] r = stack2.pop();
int[] l = stack2.pop();
int[] merged = merge(l, r);
stack.push(merged);
}
}
// odd case
if (!stack.isEmpty() && !stack2.isEmpty()) {
int[] r = stack.pop();
int[] l = stack2.pop();
int[] merged = merge(l, r);
stack.push(merged);
}
int[] sorted = stack.isEmpty() ? stack2.pop() : stack.pop();
Stack<Integer> finalStack = new Stack<>();
for (int i : sorted) {
finalStack.push(i);
}
return finalStack;
}
private int[] merge(int[] nums1, int[] nums2) {
if (nums1 == null || nums1.length == 0) {
return nums2;
}
if (nums2 == null || nums2.length == 0) {
return nums1;
}
int[] nums = new int[nums1.length + nums2.length];
int i = 0, j = 0;
for (int k = 0; k < nums.length; k++) {
if (i >= nums1.length) {
nums[k] = nums2[j];
j++;
} else if (j >= nums2.length) {
nums[k] = nums1[i];
i++;
} else if (nums1[i] <= nums2[j]) {
nums[k] = nums1[i];
i++;
} else {
nums[k] = nums2[j];
j++;
}
}
return nums;
}
}
3.3 Quick Sort with Stack
If we call the sort method with array {2,4,5,7,1,2,3,6}, it will return a stack, which contains {1,2,2,3,4,5,6,7}, 7 is at top.
import java.util.Stack;
public class StackQuickSort {
public Stack<Integer> sort(int[] nums) {
if (nums == null || nums.length == 0) {
return null;
}
quickHelper(nums, 0, nums.length - 1);
Stack<Integer> finalStack = new Stack<>();
for (int i : nums) {
finalStack.push(i);
}
return finalStack;
}
private void quickHelper(int[] nums, int start, int end) {
if (start >= end) {
return;
}
/*int pivot = partition(nums, start, end);
quickHelper(nums, start, pivot - 1);
quickHelper(nums, pivot + 1, end);*/
// use stack to implement the recursion(implicit stack).
Stack<int[]> stack = new Stack<int[]>();
stack.push(new int[] {0, end});
while (!stack.isEmpty()) {
while (start <= end) {
int pivot = partition(nums, start, end);
stack.push(new int[] {pivot + 1, end}); // execute second recursive call
end = pivot - 1; // execute first recursive call
}
int[] next = stack.pop(); // fetch next recursive call to execute
start = next[0];
end = next[1];
}
}
// one way
private int partition(int[] nums, int start, int end) {
int pivot = start; // select the first as the pivot
for (int i = start + 1; i <= end; i++) {
if (nums[i] < nums[start]) {
pivot++;
int temp = nums[pivot];
nums[pivot] = nums[i];
nums[i] = temp;
}
}
int temp = nums[pivot];
nums[pivot] = nums[start];
nums[start] = temp;
return pivot;
}
}
4. Classic Problems
- LeetCode 155 - Min Stack
- LeetCode 232 - Implement Queue using Stacks
- LeetCode 84 - Largest Rectangle in histogram
- LintCode 367 - Expression Tree Build
- LintCode 370 - Convert Expression to Reverse Polish Notation
- LintCode 368 - Expression Evaluation